Логистическая регрессия (пример)
Материал из MachineLearning.
|
Логистическая регрессия - частный случай обобщенной линейной регрессии. Предполагается, что зависимая переменная принимает два значения и имеет биномиальное распределение.
На практике логистическая регрессия используется для решения задач классификации с линейно-разделяемыми классами.
Постановка задачи восстановления логистической регрессии
Задана выборка - множество пар
, в
которых описание
-го элемента
, и
значения зависимой переменной
Принята модель логистической регрессии, согласно которой
свободные переменные и
зависимая переменная
связаны зависимостью
где .
Примем обозначения ,
вектор
Для удобства дальнейшего
изложения обозначим выборку свободных переменных как
Требуется найти такое значение вектора параметров ,
которое бы доставляло минимум норме вектора невязок
| | Исправить |
Алгоритм отыскания оптимальных параметров
Оптимальные параметры отыскиваются последовательно с помощью итерационного метода наименьших квадратов с использованием взвешивания элементов выборки. Приведенный ниже алгоритм основан на алгоритме Ньютона-Рафсона.
В начале работы алгоритма задаются параметры начального приближения:
скаляр ,
где
- среднее значение
выборки зависимой переменной и значения
для
.
Далее итеративно повторяется следующая процедура.
- С использованием вектора параметров
вычисляется переменная
- Вычисляется восстановленное значение выборки зависимой переменной
- Вычисляется вектор значений зависимой переменной для текущего шага линейной регрессии
- вектор весов значений зависимой переменной.
- Решается задача наименьших квадратов с взвешиванием элементов выборки. При этом
больший вес приобретают те элементы, которые имеют большую невязку
где диагональная матрица весов .
Процедура останавливается после того, как норма разности векторов параметров
на каждой итерации не будет превышать заданную константу:
.
Пример на модельных данных
Перед началом работы алгоритма задаются начальные значения параметров
b0 = log(mean(y)/(1-mean(y))); % 1st element, function of the mean value of y's b = [b0 zeros(size(X,2)-1,1)]'; % column-vector of parameters
Итерационное вычисление параметров логистической регрессии
while 1==1 z = X*b; % the logit^-1 variable is function of parameters p = 1./(1+exp(-z)); % recover the regression w = p.*(1-p); % calculate the weights of the samples u = z + (y-p)./w; % calculate the dependent variable for this step of least squares b_old = b; % store old parameters b = inv( X'*diag(w)*X ) * X' * diag(w) * u; % calculate new parameters with least squares % termanate the iterations if changes of the parameters are small if sumsqr(b - b_old) <= TolFun, break; end end
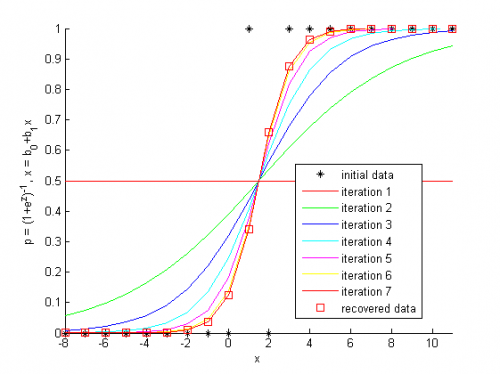
На графике показаны исходные данные. По оси абсцисс отложены значения единственного признака, а по оси ординат -- метки класса объектов. Объекты обозначены звездочками. Линии логистической кривой показывают последовательные итерации настройки параметров модели. Значения вероятности принадлежности объектов классам показаны квадратиками на кривой, которая соответствует последней итерации.
Результатом вычислительного эксперимента является иллюстрация работы алгоритма Ньютона-Рафсона для задачи восстановления логистической регрессии. Найден параметр модели, соответствующей минимуму заданной функции невязок. Получена классификация объектов, описанных единственным признаком.
Исходный код
| | Внимание! Вместо кода здесь должна быть ссылка на код! |
%% Logistic regression example % The Newton-Raphson algorithm is used to obtain the optimal parameters % of the regression model %% Create a demonstration data set % independent variable, 20 samples x = [[-8:1]'; [2:11]']; % dependent variable of zeros and ones y = [zeros(9,1); 1; 0; ones(9,1)]; % construct the matrix of independent samples X = [ones(size(x,1),1) x]; %Plot the initial data h = figure; hold on plot(X(:,2), y,'k*'); hold on txtlegend = {'initial data'}; colors = {'r-','g-', 'b-', 'c-', 'm-', 'y-'}; ncolor = 0; %% Set the constant for iteration convergence % the algorithm stops when the difference of the parameter is small TolFun = 10^-3; %% Define the initial value of the parameters % 1st element, function of the mean value of y's b0 = log(mean(y)/(1-mean(y))); % column-vector of parameters b = [b0 zeros(size(X,2)-1,1)]'; %% The Newton-Raphson procedure while 1==1 % the logit^-1 variable is function of parameters z = X*b; % recover the regression p = 1./(1+exp(-z)); % calculate the weights of the samples w = p.*(1-p); % calculate the dependent variable for this step of least squares u = z + (y-p)./w; % plot the results of this step plot(x, p, colors{mod(ncolor,length(colors))+1}); ncolor = ncolor + 1; % change color txtlegend{end+1} = ['iteration ', num2str(ncolor)]; % store old parameters b_old = b; % calculate new parameters with least squares b = inv( X'*diag(w)*X ) * X' * diag(w) * u; % termanate the iterations if changes of the parameters are small if sumsqr(b - b_old) <= TolFun, break; end end %% Show the result % claculate recovered dependent variable p = 1./(1+exp(-X*b)); % plot the result txtlegend{end+1} = 'recovered data'; plot(x, p,'rs'); legend(txtlegend); axis tight xlabel('x'); ylabel('p = (1+e^z)^{-1}, x = b_0+b_1x'); %% Notes % In Matlab there are glmfit and glmval functuions. Use them for % professional purposes. return
Смотри также
- Классификация с использованием логистической регрессии (пример)
- Логистическая регрессия
- Линейная регрессия (пример)
- Регрессионный анализ
- Метод наименьших квадратов
- Обобщенная линейная модель
- Алгоритм Ньютона
- Алгоритм Ньютона-Рафсона
- Эта статья в формате PDF
- Исходный код
Литература
- Hastie, T., Tibshirani, R., Friedman, J. The Elements of Statistical Learning, 2nd edition. — Springer, 2009. — 533 p. (подробнее)