Логистическая регрессия (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск

Strijov (Обсуждение | вклад)
(Новая: Логистическая регрессия (пример) {{TOCright}} Логистическая регрессия - частный случай [[Обобщённая лине...)
К следующему изменению →

Версия 15:05, 10 ноября 2008

Логистическая регрессия (пример)

Содержание

Логистическая регрессия - частный случай обобщенной линейной регрессии. Предполагается, что зависимая переменная принимает два значения и имеет биномиальное распределение.

На практике логистическая регрессия используется для решения задач классификации с линейно-разделяемыми классами.

Постановка задачи восстановления логистической регрессии

Задана выборка - множество m пар (\mathbf{x}_i,y_i), в которых описание i-го элемента \mathbf{x}_i\in\mathbb{R}^n, и значения зависимой переменной y\in\{0,1\}.

Принята модель логистической регрессии, согласно которой свободные переменные \mathbf{x} и зависимая переменная y связаны зависимостью

y=\text{logit}^{-1}(z)+\varepsilon=\frac{1}{1+\exp(-z)}+\varepsilon,

где z=b_0+\sum_{j=1}^nb_jx_j.

Примем обозначения p_i=f(\mathbf{b},\mathbf{x}_i), вектор \mathbf{b}=[b_0,\ldots,b_n]^T. Для удобства дальнейшего изложения обозначим выборку свободных переменных как

</p> X = \left[ \begin{array}{cc} 1 & \mathbf{x}_1^T \\ \vdots & \vdots \\ 1 & \mathbf{x}_m^T \\ \end{array} \right].

Требуется найти такое значение вектора параметров \mathbf{b}, которое бы доставляло минимум норме вектора невязок

S = \|\mathbf{y}-\mathbf{p}\|^2 = \sum_{i=1}^m(y_i-p_i)^2.

Алгоритм отыскания оптимальных параметров

Оптимальные параметры отыскиваются последовательно с помощью итерационного метода наименьших квадратов с использованием взвешивания элементов выборки. Приведенный ниже алгоритм основан на [[алгоритм Ньютона-Рафсона|алгоритме Ньютона-Рафсона]].

В начале работы алгоритма задаются параметры начального приближения: скаляр b_0=\log\frac{\tilde{y}}{1-\tilde{y}}, где \tilde{y}=\frac{1}{m}\sum_{i=1}^{m}y_i - среднее значение выборки зависимой переменной и значения b_j=0 для j=1,\ldots,n.

Далее итеративно повторяется следующая процедура.

  • С использованием вектора параметров \mathbf{b} вычисляется переменная
    \mathbf{z}=X\mathbf{b}.
  • Вычисляется восстановленное значение выборки зависимой переменной
p=\frac{1}{1+\exp(\mathbf{z})}.
  • Вычисляется вектор значений зависимой переменной для текущего шага линейной регрессии
\mathbf{u} = \mathbf{z} + \frac{\mathbf{y}-\mathbf{p}}{\mathbf{w}},
где

\mathbf{w} = \mathbf{p}(1-\mathbf{p}) - вектор весов значений зависимой переменной.

  • Решается задача наименьших квадратов с взвешиванием элементов выборки. При этом

больший вес приобретают те элементы, которые имеют большую невязку

\mathbf{b} = (X^TWX)^{-1}X^TW\mathbf{z},

где диагональная матрица весов W =\text{diag}(\mathbf{w}).

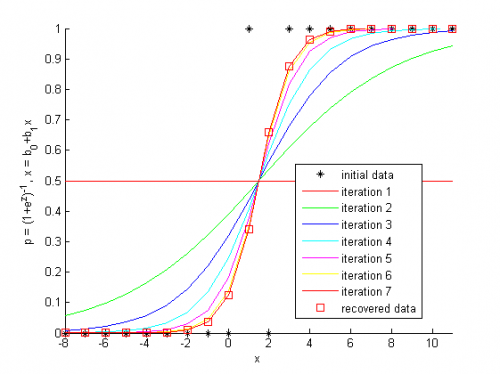
Процедура останавливается после того, как норма разности векторов весов на каждой итерации не будет превышать заданную константу: \|\mathbf{w}^{next}-\mathbf{w}^{previuos}\|^2 \leq \Delta_{w}.

Пример на модельных данных

Перед началом работы алгоритма задаются начальные значения параметров 

b0 = log(mean(y)/(1-mean(y))); % 1st element, function of the mean value of y's
b = [b0 zeros(size(X,2)-1)]';  % column-vector of parameters

Итерационное вычисление параметров логистической регрессии 

while 1==1
    z = X*b; % the logit^-1 variable is function of parameters
    p = 1./(1+exp(-z)); % recover the regression
    w = p.*(1-p); % calculate the weights of the samples
    u = z + (y-p)./w; % calculate the dependent variable for this step of least squares
    b_old = b; % store old parameters
    b = inv( X'*diag(w)*X ) * X' * diag(w) * u; % calculate new parameters with least squares
% termanate the iterations if changes of the parameters are small
if sumsqr(b - b_old) <= TolFun, break; end
end

Исходный код 

%% Logistic regression example
% The Newton-Raphson algorithm is used to obtain the optimal parameters
% of the regression model
 
%% Create a demonstration data set
 
% independent variable, 20 samples
x = [[-8:1]'; [2:11]'];
% dependent variable of zeros and ones
y = [zeros(9,1); 1; 0; ones(9,1)];
% construct the matrix of independent samples
X = [ones(size(x,1),1) x];
 
%Plot the initial data
 
h = figure;
hold on
plot(X(:,2), y,'k*'); hold on
txtlegend = {'initial data'};
colors = {'r-','g-', 'b-', 'c-', 'm-', 'y-'};
ncolor  = 0;
 
%% Set the constant for iteration convergence
 
% the algorithm stops when the difference of the parameter is small
TolFun = 10^-3;
 
%% Define the initial value of the parameters
 
% 1st element, function of the mean value of y's
b0 = log(mean(y)/(1-mean(y)));
% column-vector of parameters
b = [b0 zeros(size(X,2)-1)]';
 
%%  The Newton-Raphson procedure
 
while 1==1
    % the logit^-1 variable is function of parameters
    z = X*b;
    % recover the regression
    p = 1./(1+exp(-z));
    % calculate the weights of the samples
    w = p.*(1-p);
    % calculate the dependent variable for this step of least squares
    u = z + (y-p)./w;
 
    % plot the results of this step
    plot(x, p, colors{mod(ncolor,length(colors))+1});
    ncolor = ncolor + 1; % change color
    txtlegend{end+1} = ['iteration ', num2str(ncolor)];
 
    % store old parameters
    b_old = b;
    % calculate new parameters with least squares
    b = inv( X'*diag(w)*X ) * X' * diag(w) * u;
 
    % termanate the iterations if changes of the parameters are small
if sumsqr(b - b_old) <= TolFun, break; end
end
 
%%  Show the result
 
% claculate recovered dependent variable
p = 1./(1+exp(-X*b));
% plot the result
txtlegend{end+1} = 'recovered data';
plot(x, p,'rs');
legend(txtlegend);
axis tight
xlabel('x');
ylabel('p = (1+e^z)^{-1}, x = b_0+b_1x');
 
%% Notes
% In Matlab there are glmfit and glmval functuions. Use them for
% professional purposes.
 
return

Смотри также

Литература

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9B%D0%BE%D0%B3%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D1%8F_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»