Линейная регрессия (пример)
Материал из MachineLearning.
(→Криволинейная регрессия) |
(→Применение линейной постановки задачи для моделирования кривых второго порядка) |
||
| (12 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
| + | {{TOCright}} | ||
'''Линейная регрессия''' — метод восстановления зависимости между двумя переменными. | '''Линейная регрессия''' — метод восстановления зависимости между двумя переменными. | ||
Ниже приведен пример программы, которая строит линейную модель зависимости по | Ниже приведен пример программы, которая строит линейную модель зависимости по | ||
| Строка 8: | Строка 9: | ||
Назначена линейная [[регрессионная модель|модель]] | Назначена линейная [[регрессионная модель|модель]] | ||
<center><tex>y_i= f(\mathbf{w},x_i) + \varepsilon_i</tex></center> | <center><tex>y_i= f(\mathbf{w},x_i) + \varepsilon_i</tex></center> | ||
| - | c аддитивной [[ | + | c аддитивной [[случайная величина|случайной величиной]] <tex>\varepsilon</tex>. |
Переменные <tex>x, y</tex> принимают значения на числовой прямой <tex>\mathbb{R}</tex>. | Переменные <tex>x, y</tex> принимают значения на числовой прямой <tex>\mathbb{R}</tex>. | ||
| - | Предполагается, что | + | Предполагается, что случайная величина |
[[функция распределения|распределена]] | [[функция распределения|распределена]] | ||
| - | [[ | + | [[нормальное распределение|нормально]] с нулевым матожиданием и |
| - | фиксированной дисперсией <tex>\ | + | фиксированной дисперсией <tex>\sigma^2_\varepsilon</tex>, которая не зависит от переменных <tex>x, y</tex>. |
При таких предположениях параметры <tex>\mathbf{w}</tex> регрессионной модели вычисляются с помощью | При таких предположениях параметры <tex>\mathbf{w}</tex> регрессионной модели вычисляются с помощью | ||
[[метод наименьших квадратов|метода наименьших квадратов]]. | [[метод наименьших квадратов|метода наименьших квадратов]]. | ||
| - | Например, требуется построить зависимость цены нарезного хлеба от времени. | + | Например, требуется построить зависимость цены нарезного хлеба от времени. (См. рис. далее по тексту). |
| - | В [[Media:bread_narez_norm.doc|таблице регрессионной выборки]] первая колонка — зависимая переменная (цена батона хлеба), | + | В [[Media:bread_narez_norm.doc|таблице регрессионной выборки]] первая колонка — зависимая переменная <tex>y</tex> (цена батона хлеба), |
| - | вторая — свободная (время). Всего данные содержат 195 пар значений переменных. Данные нормированы. | + | вторая — свободная переменная <tex>x</tex> (время). Всего данные содержат 195 пар значений переменных. Данные нормированы. |
== Одномерная регрессия == | == Одномерная регрессия == | ||
| Строка 40: | Строка 41: | ||
Для оценки качества модели используется критерий суммы квадратов регрессионных остатков, | Для оценки качества модели используется критерий суммы квадратов регрессионных остатков, | ||
SSE — Sum of Squared Errors. | SSE — Sum of Squared Errors. | ||
| - | <center><tex>SSE = \sum_{i=1}^m(y_i-y_i^*) | + | <center><tex>SSE = \sum_{i=1}^m(y_i-y_i^*)^2 = (\mathbf{y}-\mathbf{y}^*)^T(\mathbf{y}-\mathbf{y}^*).</tex></center> |
| - | Пример нахождения параметров модели и восстановления линейной регрессии. | + | Пример нахождения параметров модели и восстановления линейной регрессии (здесь и далее код на языке Matlab). |
<source lang="matlab"> | <source lang="matlab"> | ||
A = [x.^0, x]; % построить матрицу подстановок | A = [x.^0, x]; % построить матрицу подстановок | ||
| Строка 62: | Строка 63: | ||
Матрица <tex>A</tex> в случае полиномиальной регрессии называется матрицей Вандермонда и | Матрица <tex>A</tex> в случае полиномиальной регрессии называется матрицей Вандермонда и | ||
принимает вид | принимает вид | ||
| - | <center><tex>A =\left(\begin{array}{ccccc} 1 & x_1 & | + | <center><tex>A =\left(\begin{array}{ccccc} 1 & x_1 & x_1^2 & \ldots & x_1^p\\ 1 & x_2 & x_2^2 & \ldots & x_2^p\\ \ldots & \ldots & \ldots & \ldots\\ 1 & x_m & x_m^2 & \ldots & x_m^p\\ \end{array} \right).</tex></center> |
Одномерная регрессия — частный случай полиномиальной регрессии. | Одномерная регрессия — частный случай полиномиальной регрессии. | ||
| Строка 191: | Строка 192: | ||
% <<regression_curve.png>> | % <<regression_curve.png>> | ||
</source> | </source> | ||
| + | |||
| + | ==Применение линейной постановки задачи для моделирования кривых второго порядка== | ||
| + | |||
| + | Постановка задачи из области контроля качества состояния трубопроводов. | ||
| + | Заданы координаты окружности (сечения трубы) -- множество точек <tex>\{(x,y)\}</tex>, измеренных с некоторой погрешностью. | ||
| + | Требуется найти центр <tex>(c_1, c_2)</tex> и радиус <tex>r</tex> окружности. | ||
| + | |||
| + | Запишем регерссионную модель-- координаты окружности относительно центра и радиуса и выделим линейно входящие компоненты: | ||
| + | |||
| + | <tex> \begin{array}{l} (x - c_1)^2 + (y - c_2)^2 = r^2,\\ 2xc_1 + 2yc_2 + (r^2-c_1^2-c_2^2) = x^2 + y^2,\\ c_3 = (r^2-c_1^2-c_2^2).\\ \end{array}</tex> | ||
| + | |||
| + | Тогда матрица плана линейной модели будет иметь вид | ||
| + | |||
| + | <tex>\left(\begin{array}{ccc}2x_1 & 2y_1 & 1 \\ 2x_2 & 2y_2 & 1 \\ \vdots & \vdots & \vdots \\ 2x_m & 2y_m & 1 \\ \end{array}\right)\left(\begin{array}{cc} c_1\\ c_2\\ c_3\\ \end{array} \right) = \left(\begin{array}{c} x_1^2 +y_1^2\\ x_2^2 +y_2^2\\ \vdots \\ x_m^2 +y_m^2\\ \end{array}\right). </tex> | ||
| + | |||
| + | Аналогичным путем получаются решения задач нахождения параметров эллипсоида, параллелограмма и других геометрических фигур. | ||
== Смотри также == | == Смотри также == | ||
| Строка 199: | Строка 216: | ||
== Литература == | == Литература == | ||
* Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Издательский дом «Вильямс». 2007. 912 с. | * Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Издательский дом «Вильямс». 2007. 912 с. | ||
| - | * Стрижов В. | + | * Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. [[Media:strijov08ln.pdf|Брошюра, PDF]]. |
== Исходный код == | == Исходный код == | ||
| Строка 205: | Строка 222: | ||
* [http://strijov.com/sources/bread_narez_norm.csv Регрессионная выборка, таблица], | * [http://strijov.com/sources/bread_narez_norm.csv Регрессионная выборка, таблица], | ||
* [http://strijov.com/sources/plot_regression_2d.m Bспомогательный файл]. | * [http://strijov.com/sources/plot_regression_2d.m Bспомогательный файл]. | ||
| + | |||
| + | [[Категория:Регрессионный анализ]] | ||
| + | [[Категория:Линейная регрессия]] | ||
| + | [[Категория:Популярные и обзорные статьи]] | ||
| + | [[Категория:Библиотеки алгоритмов]] | ||
Текущая версия
|
Линейная регрессия — метод восстановления зависимости между двумя переменными. Ниже приведен пример программы, которая строит линейную модель зависимости по заданной выборке и показывает результат на графике.
Для заданного множества из пар
,
,
значений свободной и зависимой переменной
требуется построить зависимость.
Назначена линейная модель
c аддитивной случайной величиной .
Переменные
принимают значения на числовой прямой
.
Предполагается, что случайная величина
распределена
нормально с нулевым матожиданием и
фиксированной дисперсией
, которая не зависит от переменных
.
При таких предположениях параметры
регрессионной модели вычисляются с помощью
метода наименьших квадратов.
Например, требуется построить зависимость цены нарезного хлеба от времени. (См. рис. далее по тексту).
В таблице регрессионной выборки первая колонка — зависимая переменная (цена батона хлеба),
вторая — свободная переменная
(время). Всего данные содержат 195 пар значений переменных. Данные нормированы.
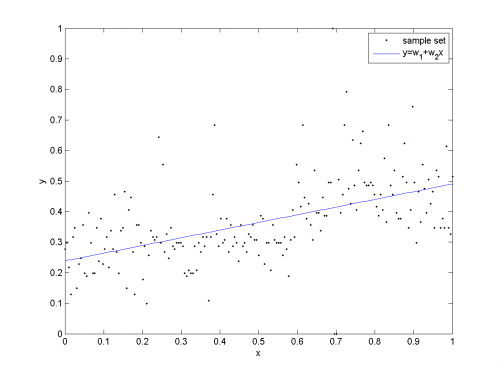
Одномерная регрессия
Определим модель зависимости как
Согласно методу наименьших квадратов, искомый
вектор параметров есть решение нормального уравнения
где — вектор, состоящий из значений зависимой переменной,
.
Столбцы матрицы
есть подстановки значений свободной переменной
и
,
. Матрица имеет вид
Зависимая переменная восстанавливается по полученным весам и заданным значениям свободной переменной
иначе
% Для оценки качества модели используется критерий суммы квадратов регрессионных остатков, SSE — Sum of Squared Errors.
Пример нахождения параметров модели и восстановления линейной регрессии (здесь и далее код на языке Matlab).
A = [x.^0, x]; % построить матрицу подстановок % x - (m,1)-вектор, у - (m,1)-вектор w = (A'*A)\(A'*y); % решить нормальное уравнение % методом гауссова исключения w = pinv(A'*A)*(A'*y);% вариант обращения матрицы y1 = w(1)+w(2)*x; % восстановить зависимую переменную % при заданных значениях x r = y-y1; % найти вектор регрессионных остатков SSE = r'*r % подсчитать ошибку
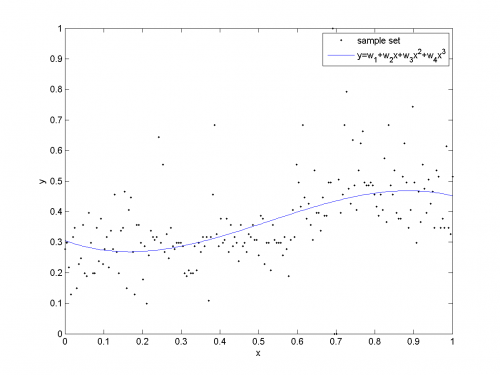
Полиномиальная регрессия
Пусть регрессионная модель — полином заданной степени ,
Матрица в случае полиномиальной регрессии называется матрицей Вандермонда и
принимает вид
Одномерная регрессия — частный случай полиномиальной регрессии.
Пример нахождения параметров модели и восстановления полиномиальной регрессии.
% функция для построения матрицы подстановок f = inline('[x.^0, x, x.^2, x.^3]','x'); A = f(x); % матрица подстановок есть функция % значений свободной переменой w = (A'*A)\(A'*y); % решить нормальное уравнение y2 = A*w; % восстановить зависимую переменную r = y-y2; % найти вектор регрессионных остатков SSE = r'*r % подсчитать ошибку
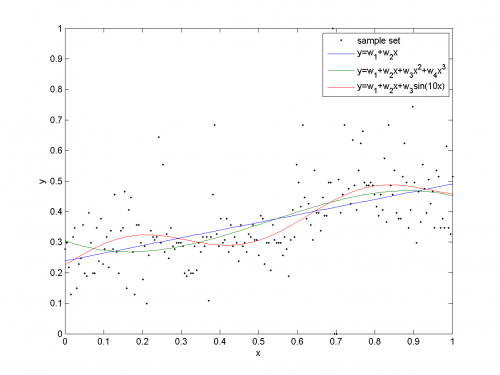
Криволинейная регрессия
Пусть исходные признаки преобразованы с помощью некоторых заданных, в общем случае нелинейных
функций . При этом функции не должны содержать дополнительных
параметров. Функции должны быть определены на всей числовой прямой, либо, по крайней мере, на
всех значениях, которые принимает свободная переменная.
Матрица в случае полиномиальной регрессии называется обобщенной матрицей Вандермонда и
принимает вид
Полиномиальная регрессия — частный случай криволинейной регрессии.
Пример нахождения параметров модели и восстановления криволинейной регрессии.
% функция для построения матрицы подстановок f = inline('[x.^0, x, sin(10*x)]','x'); A = f(x); % матрица подстановок w = (A'*A)\(A'*y); % решить нормальное уравнение y3 = A*w; % восстановить зависимую переменную r = y-y3; % найти вектор регрессионных остатков SSE = r'*r % подсчитать ошибку
Исходный код
(Этот раздел должен быть скрыт)
%% Линейная регрессия % Исходный код к статье "Линейная регрессия (пример)" % www.machinelearning.ru %% Получить данные из файла % В файле содержаться цены на хлеб "нарезной" за несколько месяцев D = dlmread('bread_narez_norm.doc'); y = D( :,1); % в первом столбце значения зависимой переменной x = D( :,2); % во втором столбце - независимой %% Смоделировать исходные данные % Если файл данных отстутствует, можно создать данные самостятельно % x = linspace(0,10,200)'; % независимая переменная, значения % y = x + 1.5*sin(x) + randn(size(x,1),1); % зависимая переменная имеет % наложенную случайную переменную с нулевым матожиданием и однородной % дисперсией %% Настроить параметры графиков % Используется внешняя функция plot_regression_2d %pltopts.xdate='on'; % ось абсцисс - дата pltopts.ftype={'psc2', 'png'}; % записать графиков файлы в формате .eps и .png %% Одномерная регрессия % Восстанавливаемая регрессионная зависимость - прямая на плоскости. model1 = 'y=w_1+w_2x'; A = [x.^0, x]; % построить матрицу подстановок % x - (m,1)-вектор, у - (m,1)-вектор w = (A'*A)\(A'*y); % решить нормальное уравнение % методом гауссова исключения w = pinv(A'*A)*(A'*y);% вариант обращения матрицы y1 = w(1)+w(2)*x; % восстановить зависимую переменную % при заданных значениях x r = y-y1; % найти вектор регрессионных остатков SSE = r'*r % подсчитать ошибку % нарисовать график pltopts.legend = {'sample set',model1}; pltopts.fname = 'regression_onedim'; plot_regression_2d(x,[y y1], pltopts); %% % <<regression_onedim.png>> %% Полиномиальная регрессия % Восстанавливаемая зависимость - кубическая кривая model2 = 'y=w_1+w_2x+w_3x^2+w_4x^3'; % функция для построения матрицы подстановок f = inline('[x.^0, x, x.^2, x.^3]','x'); A = f(x); % матрица подстановок есть функция % значений свободной переменой w = (A'*A)\(A'*y); % решить нормальное уравнение y2 = A*w; % восстановить зависимую переменную r = y-y2; % найти вектор регрессионных остатков SSE = r'*r % подсчитать ошибку % нарисовать график pltopts.legend = {'sample set',model2}; pltopts.fname = 'regression_poly'; plot_regression_2d(x,[y y2], pltopts); %% % <<regression_poly.png>> %% Криволинейная регрессия % Восстанавляваемая зависимость, кроме мнономов, содержит другие функции, % нелинейные относительно независимой переменной model3 = 'y=w_1+w_2x+w_3sin(10x)'; f = inline('[x.^0, x, sin(10*x)]','x'); A = f(x); % матрица подстановок w = (A'*A)\(A'*y); % решить нормальное уравнение y3 = A*w; % восстановить зависимую переменную r = y-y3; % найти вектор регрессионных остатков SSE = r'*r % подсчитать ошибку % нарисовать график pltopts.legend = {'sample set', model1, model2, model3}; pltopts.fname = 'regression_curve'; plot_regression_2d(x,[y y1 y2 y3], pltopts); %% % <<regression_curve.png>>
Применение линейной постановки задачи для моделирования кривых второго порядка
Постановка задачи из области контроля качества состояния трубопроводов.
Заданы координаты окружности (сечения трубы) -- множество точек , измеренных с некоторой погрешностью.
Требуется найти центр
и радиус
окружности.
Запишем регерссионную модель-- координаты окружности относительно центра и радиуса и выделим линейно входящие компоненты:
Тогда матрица плана линейной модели будет иметь вид
Аналогичным путем получаются решения задач нахождения параметров эллипсоида, параллелограмма и других геометрических фигур.
Смотри также
Литература
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Издательский дом «Вильямс». 2007. 912 с.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.