Система линейных алгебраических уравнений

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

Система m линейных алгебраических уравнений с n неизвестными — это система уравнений вида

\left\{\begin{array}{ccccccccc} a_{11}x_1 & + & a_{12}x_2 & + & \ldots & + & a_{1n}x_n & = & b_1, \\ a_{21}x_1 & + & a_{22}x_2 & + & \ldots & + & a_{1n}x_n & = & b_2, \\ \vdots & & \vdots & & & & \vdots & & \vdots \\ a_{m1}x_1 & + & a_{m2}x_2 & + & \ldots & + & a_{1n}x_n & = & b_m. \\ \end{array}\right.

Здесь x_1, x_2, \ldots, x_n — неизвестные, которые надо определить. Коэффициенты системы a_{11}, a_{12}, \ldots, a_{mn} и её свободные члены b_1,b_2,\ldots,b_m предполагаются известными. Индексы коэффициента a_{ij} системы обозначают номера уравнения i и неизвестного j, при котором стоит этот коэффициент.

Система называется однородной, если все её свободные члены равны нулю, b_1=b_2=\ldots=b_n=0, иначе — неоднородной.

Система называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы уравнений — совокупность n чисел c_1,c_2,\ldots,c_n, таких что подстановка каждого c_i вместо x_i в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.

Решения c_1,c_2,\ldots,c_n и c'_1, c'_2,\ldots,c'_n совместной системы называются различными, если нарушается хотя бы одно из равенств:

c_1=c'_1,c_2=c'_2,\ldots,c_n=c'_n.

Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как

A\mathbf{x} = \mathbf{b},

где

A= \begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{pmatrix},\mathbf{x}=\begin{pmatrix}x_1 \\ x_2 \\ \vdots\\x_n\end{pmatrix},\mathbf{b}=\begin{pmatrix}b_1 \\b_2 \\ \vdots \\b_m\end{pmatrix}.

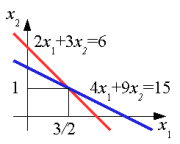
Пример системы линейных уравнений

Графическое решение системы линейных уравнений
Графическое решение системы линейных уравнений

Система из двух уравнений с двумя неизвестными имеет вид

\left\{\begin{array}{ccccc} 2x_1 & + & 3x_2 & = & 6,\\ 4x_1 & + & 9x_2 & = & 15.\\ \end{array}\right.

Чтобы найти неизвестные x_1,x_2 нужно решить верхнее уравнение относительно x_1: x_1=3-\frac{3}{2}x_2, а затем подставить полученное решение в нижнее уравнение: 4\left(3-\frac{3}{2}x_2\right)+9x_2=15. Получено решение x_1=\frac{3}{2}, x_2=1.

Данную систему можно наглядно изобразить на графике в виде двух прямых. Точка с координатами (\frac{3}{2},1) является ее решением.

Методы решения

Прямые (или точные) методы решения СЛАУ позволяют найти решение за определенное количество шагов. К прямым методам относятся метод Гаусса, метод Гаусса — Жордана, метод Крамера, матричный метод и метод прогонки (для трёхдиагональных матриц).

Итерационные методы основаны на использовании повторяющегося процесса. Они позволяют получить решение в результате последовательных приближений. К итерационным методам относятся метод Якоби (метод простой итерации), метод Гаусса — Зейделя, метод релаксации и многосеточный метод.

Смотри также

Применение систем линейных уравнений

Внешние ссылки

Литература

  • Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. М.: Наука 1986. 304с.
  • Гельфанд И.М. Лекции по линейной алгебре М.: Наука. 1971.
  • Шилов Г.Е. Математический анализ (Конечномерные линейные пространства). 264с.
  • Малоземов В.Н. Линейная алгебра без определителей. Квадратичная функция: учеб. пособие. СПб.: Изд-во С.-Петерб. ун-та, 1997. 80с.
  • Стренг Г. Линейная алгебра и ее применения. М.:Мир 1980. 454с.
  • Мальцев А.И. Основы линейной алгебры. М.: Наука. 1975.
  • Фаддеев Д.К. Лекции по алгебре. М.: Наука. 1984.
  • Ильин В.А., Позняк Э.Г. Линейная алгебра, М.: Наука-Физматлит. 1999.
  • Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия, М.: ТК Велби, Изд во Проспект, 2007, 400с.
  • Беклемишев Д.В. Аналитическая геометрия и линейная алгебра. М.: Высш. шк. 1998. 320с.
  • Беклемишев Д.В. Дополнительные главы линейной алгебры. М.:Наука 1983. 336с.
  • Булдырев В.С., Павлов Б.С. Линейная алгебра и функции многих переменных. Л.: ЛГУ 1985. 496с.
  • Гантмахер Ф.Р. Теория матриц. М.: Наука 1966. 576с.
  • Гельфанд И.М., Линейная алгебра. Курс лекций.
  • Ефимов Н.В. Розендорн Э.Р. Линейная алгебра и многомерная геометрия. М.: Наука 1969. 528с.
  • Кострикин А.И. Введение в алгебру, М.: Наука. 1977.
  • Курош А.Г. Курс высшей алгебры. М.: Наука 1968. 331с.
  • Ланкастер П. Теория матриц. М.: Наука 1973. 280с.
  • Проскуряков И.В. Сборник задач по линейной алгебре. М.: Наука 1966. 384с.
  • Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. 356с.
  • Халмош П. Конечномерные векторные пространства. М.: Физматгиз 1963. 264с.
  • Хорн Р., Джонсон Ч. Матричный анализ. 655с.
  • Тыртышников Е. Е. Матричный анализ и линейная алгебра. Курс лекций для студентов факультета ВМК, МГУ.
Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D1%8B%D1%85_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B9»
Личные инструменты