Профиль компактности

Материал из MachineLearning.

Версия от 22:07, 22 сентября 2008; Vokov (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Определения
2 Связь с полным скользящем контролем
3 См. также
4 Литература

Профиль компактности выборки в метрических алгоритмах классификации — функция $R(j)$ , выражающая долю объектов выборки, для которых правильный ответ не совпадает с правильным ответом на $j$ -м соседе.

Определения

Рассматривается задача классификации. Имеется множество объектов $X$ и множество имён классов $Y$ . Задана обучающая выборка пар «объект—ответ» $X^m = \{(x_1,y_1),\ldots,(x_m,y_m)\} \in X\times Y$ .

Пусть на множестве объектов задана функция расстояния $\rho(x,x')$ . Эта функция должна быть достаточно адекватной моделью сходства объектов. Чем больше значение этой функции, тем менее схожими являются два объекта $x,x'$ .

Для произвольного объекта $u$ расположим объекты обучающей выборки $x_i$ в порядке возрастания расстояний до $u$ :

$\rho(u,x_{1; u}) \leq \rho(u,x_{2; u}) \leq \cdots \leq \rho(u,x_{m; u}),$

где через $x_{i; u}$ обозначается элемент обучающей выборки, который является $i$ -м соседом объекта $u$ . Аналогичное обозначение введём и для ответа на $i$ -м соседе: $y_{i; u}$ . Каждый объект $u\in X$ порождает свою перенумерацию выборки.

Рассматривается метод ближайшего соседа, который относит классифицируемый объект $u$ к тому классу $y_i$ , которому принадлежит ближайший объект обучающей выборки $x_i$ :

$a(u,X^m) = y_{1;u}.$

Определение. Профиль компактности выборки $X^m$ есть функция

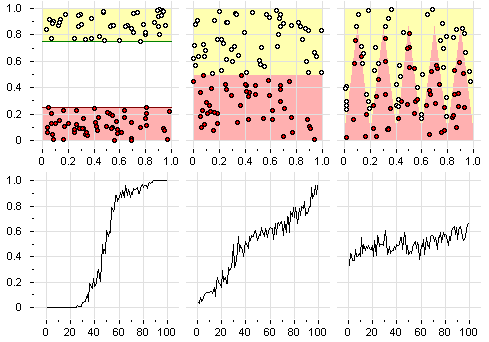
$R(j,X^m) = \frac1m \sum_{i=1}^L \left[ y_i \neq y_{j;x_i} \right].$

Профиль компактности является формальным выражением гипотезы компактности — предположения о том, что схожие объекты гораздо чаще лежат в одном классе, чем в разных. Чем проще задача, то есть чем чаще близкие объекты оказываются в одном классе, тем сильнее «прижимается к нулю» начальный участок профиля. В сложных задачах или при неудачном выборе функции расстояния ближайшие объекты практически не несут информации о классах, и профиль вырождается в константу, близкую к 0.5.

На рисунке показаны профили компактности для серии плоских модельных задач классификации с двумя классами. Чем ниже проходит начальный участок профиля, тем выше обобщающая способность метода ближайшего соседа.

Связь с полным скользящем контролем

Выборка $X^L$ разбивается всевозможными $N=C_L^k$ способами на две непересекающиеся подвыборки: $X^L = X^m_n \cup X^k_n$ , где $X^m_n$ — обучающая подвыборка длины&nbps;m, $X^k_n$ — контрольная подвыборка длины $k=L-m$ , $n=1,\ldots,N$ — номер разбиения.

Для каждого разбиения n строится алгоритм $a_n(u,X^m_n)$ . Функционал полного скользящего контроля (complete cross-validation, CCV) определяется как средняя (по всем разбиениям) ошибка на контроле:

$CCV(X^L)=\frac1N \sum_{n=1}^N \sum_{x_i \in X^k_n} \left[ a_n(x_i,X^m_n) \neq y_i \right].$

Функционал полного скользящего контроля характеризует обобщающую способность метода ближайшего соседа

Теорема. Справедлива формула для эффективного вычисления CCV через профиль компактности:

$CCV(X^L)= \sum_{j=1}^k R(j) \Gamma(j),$

где $\Gamma(j) = \frac{C_{L-1-j}^{m-1}}{C_{L-1}^{m}}.$

Комбинаторный множитель $\Gamma(j)$ быстро убывает с ростом $j$ . Поэтому для минимизации функционала CCV достаточно, чтобы при малых j профиль принимал значения, близкие к нулю. Но это и означает, что близкие объекты должны лежать преимущественно в одном классе. Таким образом, профиль действительно является формальным выражением гипотезы компактности.