Выбор оптимального алфавита марковских моделей для распознавания речи (отчет)

Материал из MachineLearning.

Версия от 12:25, 3 октября 2013; Mikethehuman (Обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Перейти к: навигация, поиск

Введение в проект

Описание проекта

Цель проекта

Построение дерева скрытых марковских моделей (СММ) аллофонов.

Обоснование проекта

Полученные данные могут быть использованы в качестве словаря аллофонов в масштабных дикторонезависимых системах распознавания слитной русской речи.

Описание данных

В качестве речевого материала используется обучающая выборка базы данных TeCoRus, предназначенная для приложений, использующих телефонный канал связи. Обучающая выборка представляет собой шестичасовую запись чтения 6 дикторами и состоит из 510 отдельных предложений, отсегментированных и размеченных вручную. Звуковые данные перведены в мел-кепстральное представление, т.е. последовательность 12 компонентных мел-кепстральных векторов с шириной окна квантования 512 точек.

Критерии качества

Критерием качества служит логарифм правдоподобия контрольной выборки относительно модели.

Требования к проекту

Логарифм правдоподобия для нашего дерева должн быть больше логарифма правдоподобия для базового. В качестве базового выбран набор марковских моделей соответсвующих фонемам русского языка.

Выполнимость проекта

Сложность распознавания ухудшается высокой вариативностю произношения одних и тех же звуков, а так же различными артикулярными характеристиками речевого аппарата у разных дикторов. Так же в данных присутсвует фоновый шум.

Используемые методы

В данной работе для статистического моделирования спектральной динамики гласных и согласных звуков применяется скрытая марковская модель (СММ) из 3-х последовательных состояний. Классификация аллофонов осуществляется с помощью бинарных деревьев. Построение дерева осуществляется алгоритмом ID3.

Постановка задачи

Вход:

Обучающая выборка $X$ , элементы которой $x_i = \{ M, C \}$ , где $M$ последовательность 12 мел-кепстральных векторов соответствует звуковой реализации фонемы, а $C = \{c_{left}, c_{center}, c_{right} \}$ - правый, левый контекст аллофона и центральный элемент.

Список бинарных вопросов $Q$ адресованных к центральному элементу аллофона. Служит множеством элементарных предикатов при построении бинарного дерева.

Выход:

Бинарное дерево скрытых марковских моделей аллофонов $T$ .

Функционал качества:

Логарифм правдоподобия выборки $\{X\}_1^n$ относительно модели $\lambda$ есть $LL = \sum_{i=1}^n \log P(M_i|\lambda)$

Критерии останова:

Приращение $\Delta LL$ меньше порога, или число элементов выборки в вершине меньше порогового.

Базовые предположения или гипотезы, лежащие в основе алгоритма

В настоящей работе для моделирования спектральной динамики гласных и согласных используется СММ, которая позволяет представить звук в виде последовательных состояний, соотносимых счленением звука на сегменты (субаллофоны). Внашем случае фонема разделяется на три отрезка (начальный и конечный формантные переходы плюс вокалическое ядро). Поэтому СММ имеет три состояния $Q = 3$ и лево-правую матрицу переходных вероятностей $A = \{a_{ij}\}$ .

Математическое описание алогритмов

Обучение скрытой марковской модели (СММ)

Составляющие СММ:

1. $Q$ — общее количество состояний в модели. В нашей задаче $Q = 3$ . Мы обозначим совокупность состояний модели множеством $S = \left\{ S_1, S_2, \ldots S_N \right\}$ , а текущее состояние в момент времени $t$ как $q_t$ .

2. Матрица вероятностей переходов $A = \{ a_{ij} \}$ , где

$a_{ij} = P \left[ q_{t+1} = S_j | q_t =S_i \right],\; 1 \le i, j \le N,$

то есть это вероятность того, что система, находящаяся в состоянии $S_i$ , перейдет в состояние $S_j$ . В контексте нашей задачи используется лево-правая матрица переходов. То есть $a_{ii} > 0$ и $a_{j,j+1} > 0$ для $1 \le i \le N,\; 1 \le j \le N-1$ . В остальных состояниях вероятность перехода $a_{ij} = 0$ .

3. $b_i(O) = \sum_{m=1}^M c_{jm} N(O, \mu_{jm}, \Sigma_{jm}), 1 \le i, j \le N$ ,

где $O$ - моделируемый вектор наблюдений, $c_{jm}$ - весовой коэффициент $m$ -й компоненты в состоянии $j$ .

$N(O, \mu_{jm}, \Sigma_{jm})$ - гауссова плотность вероятности с вектором средних значений $\mu_{jm}$ и ковариационной матрицей $\Sigma_{jm}$ .

4. Распределение вероятностей начального состояния $\pi = \left\{ \pi_i \right\}$ , где $\pi_i = P[q_1 = S_i], 1 \le i \le N,$ то есть вероятность того, что $S_i$ это начальное состояние модели. В нашем случае всегда начинаем с 1-го состояния т.е. $\pi_1 = 1$

Совокупность значений $Q,A,B$ и $\pi$ - это скрытая марковская модель, которая может сгенерировать наблюдаемую последовательность.

Для решения задачи обучения СММ требуется подобрать параметры модели $\lambda = (A,B,\pi)$ таким образом, чтобы максимизировать $P(O | \lambda)$ . В этой работе используется метод Баума-Уэлча, EM-метод переоценки параметров СММ. Формулы повторного оценивания для коэффициентов $c_{jm}$ , $\mu_{jm}$ и $\Sigma_{jm}$ , составляющих плотности имеют вид.

$\vec{c}_{jk} = \frac{\sum_{t=1}^T \gamma_t(j,k)}{\sum_{t=1}^T \sum_{k=1}^M \gamma_t(j,k)}$

$\vec{\mu}_{jk} = \frac{\sum_{t=1}^T \gamma_t(j,k) O_t}{\sum_{t=1}^T \gamma_t(j,k)}$

$\vec{\Sigma}_{jk} = \frac{\sum_{t=1}^T \gamma_t(j,k) (O_t - \mu_{jk})(O_t - \mu_{jk})\prime}{\sum_{t=1}^T \gamma_t(j,k)}$ ,

где штрих означает транспонирование вектора, а $\gamma_t(j,k)$ - вероятность того,что (при заданной последовательности наблюдений) в момент времени $t$ модель находиться в состоянии $j$ , причём наблюдаемый в этот момент вектор $O_t$ порождён $k$ -й компонентой смеси плотности, т.е.

$\gamma_t(j,k) = \left( \frac{\alpha_t(j) \beta_t(j)}{\sum_{j=1}^N \alpha_t(j) \beta_t(j)} \right) \left( \frac{c_{jk} N(O, \mu_{jm}, \Sigma_{jm})}{\sum_{m=1}^M c_{jm} N(O, \mu_{jm}, \Sigma_{jm})} \right)$ ,

где $\alpha_t(i) = P(O_1 O_2 \ldots O_t, q_t = S_i|\lambda)$ - прямая переменная, а $\beta_t(i) = P(O_{t+1} O_{t+2} \ldots O_t, q_t = S_i|\lambda)$ - обратная переменная.

Алгоритм построения решающего дерева ID3

В качетсве основного алгоритма использовался рекурсивный алгоритм синтеза бинарного решающего дерева ID3. Идея заключается в последовательном дроблении выборки на две части до тех пор, пока дальнейшее расщепление не перестанет давать достаточное приращение информативности.

Процедура LearnID3 выглядит следующим образом

Вход:

$U$ - выборка из последовательностей мел-кепстральных векторов соответсвующих фонеме;

$Q$ - множество вопросов к контесту фонемы, расщепляющих выборку на 2 класса.

Выход:

возвращает корневую вершину дерева $T$

найти предикат с максимальной информативностью: $q = \arg\max_{q\in Q} I(q,U)$
разбить выборку на две части $U = U_0 \cup U_1$ по предикату $q$ ;
eсли ( $U_0$ = ∅ или $U_1$ = ∅ ) или $I(q,U)$ ≤ $I_0$ то
создать новый лист $v$ .
иначе
создать новую вершину $v$ ;
$L_v = LearnID3(U_0)$ ; (построить левое поддерево)
$L_r = LearnID3(U_1)$ ; (построить правое поддерево)
вернуть $(v)$

Для построения полного дерева рекурсивная процедура LearnID3 применяется ко всей выборке.

В качаестве критерия ветвления используется максимум приращения логарифма правдоподобия при ращеплении $\Delta LL = (LL_l + LL_r) - LL_p$ , где $LL_p$ - логарифм правдоподобия родительской вершины, а $LL_l$ и $LL_r$ - логарифм правдоподобия левой и правой дочерней вершин соответственно. Логарифм правдоподобия выборки $\{X\}_1^n$ относительно СММ $\lambda$ есть $LL = \sum_{i=1}^n \log P(M_i|\lambda)$ считается алгоритмом прямого-обратного хода. Т.е для каждого вопроса выборка из родительского узла разбивается на 2 части, на каждой части обучается СММ. Считается приращение $\Delta LL$ и выбирется вопрос дающий максимальное приращение информативности.

Множество вопросов к контексту фонемы (элементарных предикатов) $Q$ задается шаблоном:

left-center+right,

где left и right - названия классов левого и правого контекста, а center - имя класса центрального элемента, * - любая фонема. Например вопрос выделяющий все гласные:

*-ALL_VOWELS+*.

Предредукция или критерий раннего останова досрочно прекращает ветвление, если максимальное приращение информативности $I(q,U)$ меньше порогового $I_0$ .

Описание системы

Описание системы находится в файле Systemdocs.doc Файлы системы можно скачать здесь: BuildTreeAllophone

Отчет о вычислительных экспериментах

Выбор оптимальных значений параметров алгоритма

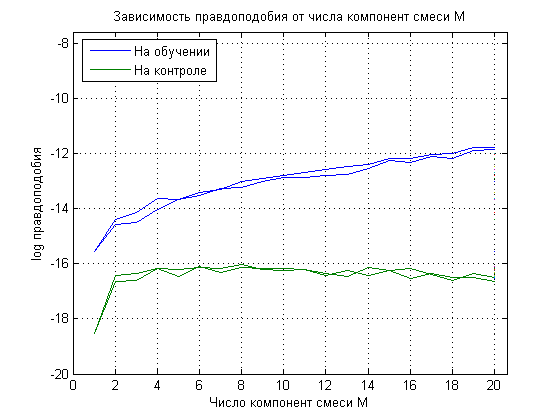
Выбор оптимального количества компонент смеси. Вычисления проводились дважды, видно что есть небольшой разброс. Оптимальный параметр M = 6.

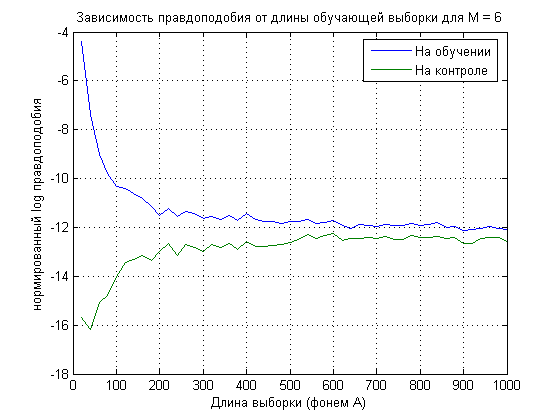
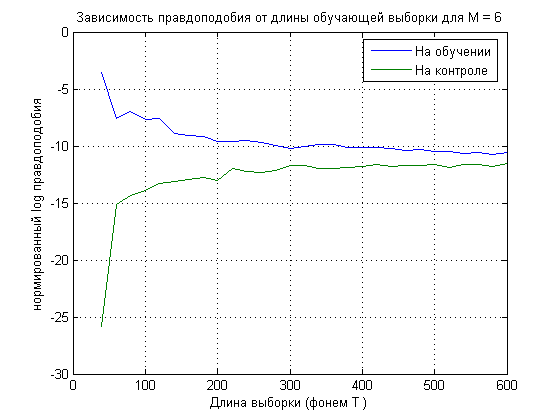
Выбор минимального размера представительной выборки для гласных (фонемы А) и согласных (Т) минимальный размер равен примерно 200 фонем.

Отчет о полученных результатах

Фрагмент дерева (первые 3 уровня), правая ветвь ответ на вопрос к контексту фонемы ДА, левая - НЕТ Формат представления вершин следующий:

для узлов

название_вопроса
[NNNNx -xx.x]

где NNNNx - число элементов в вершине, -xx.x - нормированный логарифм правдоподобия

для терминальных вершин

{список превалирующих фонем} 
[NNNNx -xx.x]

                                             ALL_HARD_CONS_FRONT
                                             [1696x, -10.6]
                              ALL_NASAL
                              [7345x, -13.4]
                              |              ALL_LATERALS
                              |              [5649x, -13.5]
               ALL_HARD_CONS_VOICED
               [26379x, -14.5]
               |              |              ALL_SOFT_CONS_VOICELESS
               |              |              [6476x, -13.7]
               |              ALL_SOFT_CONS
               |              [19034x, -14.0]
               |                             ALL_HARD_CONS
               |                             [12558x, -13.4]
ALL_CONS
[39983x, -15.0]
               |                             { W  I  E  A  O }
               |                             [820x, -12.3]
               |              L_ALL_SOFT_NASAL
               |              [5308x, -12.8]
               |              |              L_ALL_SOFT_CONS_VOICELESS
               |              |              [4488x, -12.5]
               L_ALL_SOFT_CONS
               [13604x, -14.1]
                              |              { A  U  JA  Y  O }
                              |              [635x, -12.2]
                              R_PHRASE_BOUNDARY
                              [8296x, -14.0]
                                             L_ALL_HARD_BILAB
                                             [7661x, -13.7]

Вопрос представляет собой следующее (* - любая фонема) например:

L_ALL_SOFT_CONS = ALL_SOFT_CONS-*+*

где ALL_SOFT_CONS класс фонем

ALL_SOFT_CONS = {B' P' D' T' G' K' CH' JH' V' F' Z' S' X' XV' ZH' SH' M' N' L' R' J'}

Список литературы

К. В. Воронцов, Лекции по логическим алгоритмам классификации
Л. Рабинер, Скрытые марковские модели, ТИИЭР №2, февраль 1989
Рабинер, Шафер, Цифровая обработка речевых сигналов, М., Радио и связь, 1980
X. Huang, A. Acero, H. Hon, Spoken Language Processing, A Guide to Theory, Algorithm and System Development, Prentice-Hall Inc, 2001