Долгосрочное прогнозирование ежедневных цен на электроэнергию (пример)

Материал из MachineLearning.

Версия от 21:43, 26 октября 2010; Raisa (Обсуждение | вклад)
(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск

Содержание

Постановка задачи

У нас есть временной ряд из матрицы X признаков и вектора Y ответов. Нам необходимо восстановить вектор ответов \hat{Y} по матрице признаков \hat{X}. Известно, что временной ряд, который необходимо восстановить идет непосредственно после временного ряда, ответы для которого нам известны.

Предлагается использовать функционал качества MAPE:

{ Q(\hat{Y}) = \sum_{i=1}^n \frac{|y_i-\hat{y}_i|}{|y_i|},

где \hat{Y} = (\hat{y}_1, \hat{y}_2, \dots, \hat{y}_n ) -- восстановленные ответы, а Y = (y_1, y_2, \dots , y_n) -- правильные ответы.

Описание данных

У нас есть данные с 01/01/2003 до сегодняшнего дня. Данные для прогнозирования состоят из временного ряда, различных погодных параметров (температура, скорость ветра, относительная влажность, ...) и средних цен на электричество.

В нашей задаче мы используем следующие данные - матрицу переменных xRegression и вектор откликов yRegression. Мы будем обозначать их X и Y соответственно. Размер X -- n\times m, где n -- количество объектов (временной ряд дней), а m -- количество переменных. Размер Y -- n\times 1.

Первый столбец X и Y -- временной ряд. Второй столбец Y -- вектор откликов. Они нормализованы на среднегодичное значение. Количество переменных в X -- 26. Они представлены в таблице ниже.

# Описание
1 временной ряд
2-6 день недели
7-18 месяц
19 средняя температура
20 индекс HDD
21 индексCDD
22 максимальная температура
23 минимальная температура
24 относительная влажность
25 осадки
26 скорость ветра

Предположения о характере данных

  • Предполагается, что отсчеты времени сделаны через равные промежутки.
  • Предполагается, что ряд имеет периодическую составляющую.
  • Предполагается, что ряд имеет пропущенные значения.
  • Предполагается, что длина ряда кратна периоду. Это условие можно достичь, присоединив к началу ряда необходимое число пропущенных значений.

В нашем случае, данные имеют ярко выраженную годовую периодическую составляющyю. Это можно проследить на примере данных о средней температуре за день. 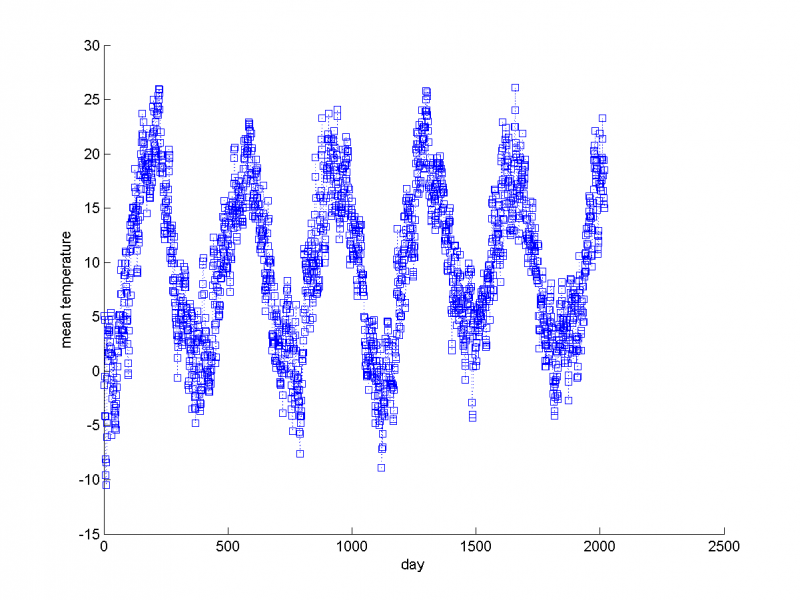Data-mean_temp.png


Пути решения задачи

  • Данные имеют годовую периодику. Будем выполнять прогноз с горизонтом прогноза, равным длине периода, при помощи авторегрессии.
  • Параметры модели, с помощью которых выполняется прогноз вектора Y, находятся с помощью алгоритма LARS.

Авторегрессия

Построение авторегрессионной матрицы. Дан временной ряд x=\begin{Vmatrix} x_1 \\ x_2 \\ \vdots \\ x_T \end{Vmatrix} .

Составляется (m {X} k) -матрица значений временного ряда:

X=\begin{Vmatrix} x_T & x_T-1 \cdots & x_T-k+1 \\ x_(m-1)k & x_(m-1)k-1 \cdots & x_(m-2)k+1 \\ \vdots \\ x_k & x_k-1 \cdots & x_1\\ \end{Vmatrix} , в которой длина ряда T= mk .

Обозначим столбцы матрицы x_k, \cdots x_1\\ . Для каждого столбца i матрицы X построим набор моделей-предикатов. Для это зафиксируем столбец x_i , считая, что прогнозируеем значение ряда в момент времени i+k .

Для каждого из прочих столбцов x_j, j= 1 \cdots ,k\\ решим задачу линейной регрессии |x_i-\mathbf{G_jw}\|^2\longrightarrow\min , где матрица

X=\begin{Vmatrix} g_1(x_mj) & g_2(x_mj) \cdots & g_r(x_mj) \\ g_1(x_(m-1)j & g_2(x_(m-1)j) \cdots & g_r(x_(m-1)j \\ \vdots \\ g_1(x_j) & g_2(x_j) \cdots & g_r(x_j)\\ \end{Vmatrix}

Функции g_1, \cdots , g_r заданы или определены, исходя из дополнительных условий.

Выбирается заданное число p векторов G_jw , доставляющих наибольшее значение функционалу качества. Обозначим P - множество выбранных индексов {j} . Строится корректор над множеством моделей-предикатов- линейная регрессия |x_i-\mathbf{H_pb}\|^2\longrightarrow\min с ограничением на неотрицательность векторов b . Матрица H_p - присоединённые векторы G_jw . Прогнозируемое значение ряда x в момент времени k+i равно значению первого элемента вектора H_pb .


Вычислительный эксперимент

Авторегрессия

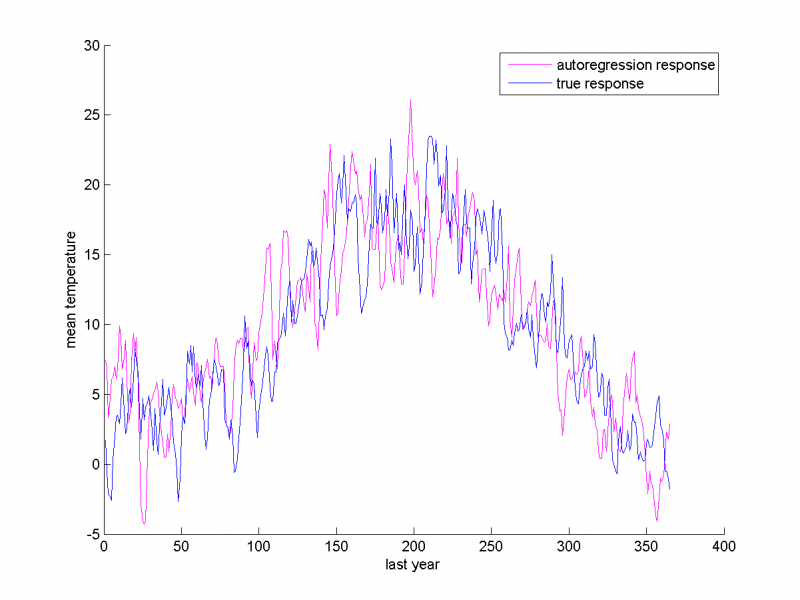
Выборка разбивается на обучающую и тестовую. Тестовой выборкой являются данные за последний год. Прогнозирование выполняется с помощью построения авторегрессионной матрицы. На примере нескольких временных рядом посмотрим, как реальные данные соотносятся с прогнозируемыми.

Cредняя температура

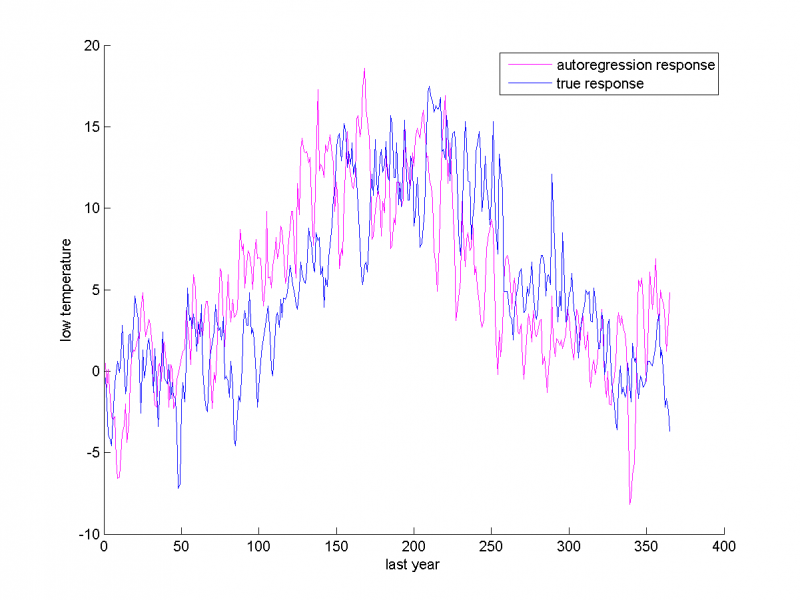
Минимальная температура

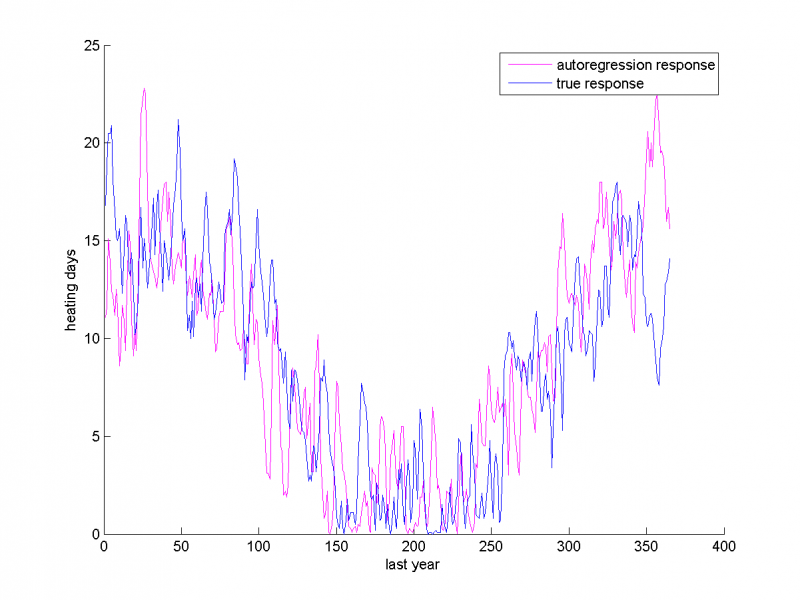
Индекс HDD


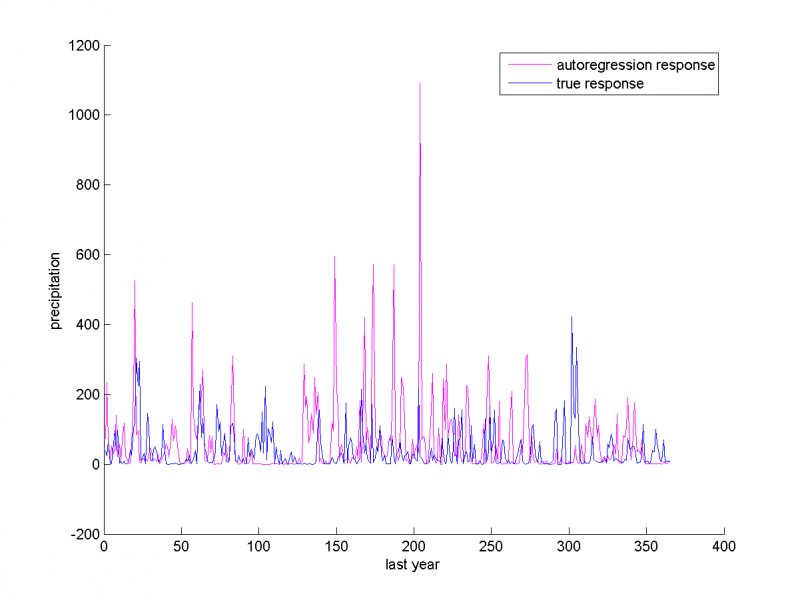
Осадки


LARS

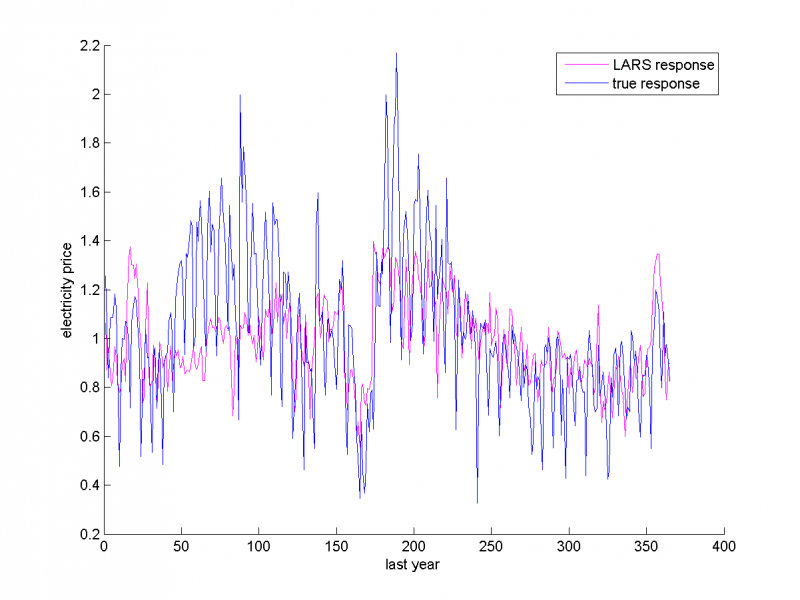
Выборка разбивается на обучающую и тестовую. Тестовой выборкой являются данные за последний год. Вектор Y находим с помощью алгоритма LARS.Проверим, насколько реальные данные соотносятся с прогнозируемыми.

График LARS

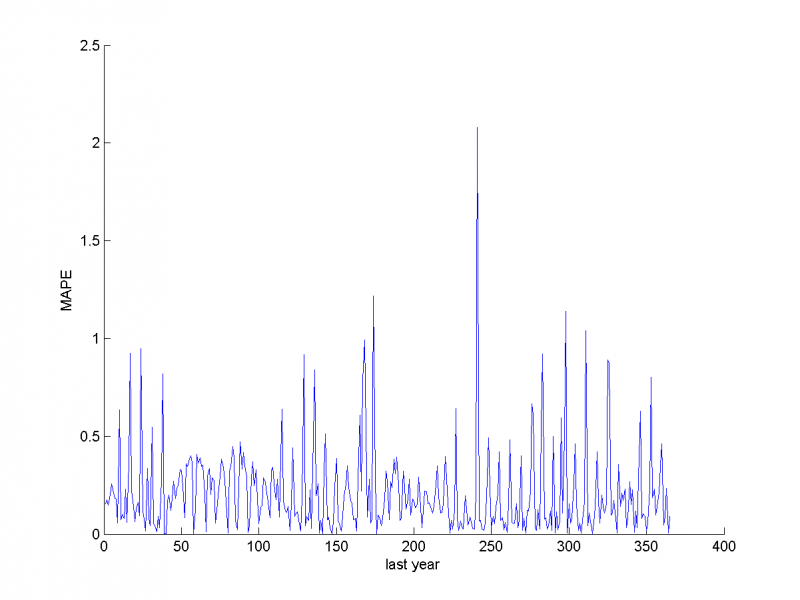
График MAPE

Код

autoregression.m


lars.m

Смотри также

Литература

  1. Vadim Strijov Model Generation and its Applications in Financial Sector. — 2009.
  2. Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani Least Angle Regression. — 2002.
  3. Стрижов В.В Методы выбора регрессионных моделей. — 2010.
  4. Rafal Weron Modeling and Forecasting Electricity Loads and Prices. — 2006.
Источник — «http://www.recognition.su/wiki/index.php?title=%D0%94%D0%BE%D0%BB%D0%B3%D0%BE%D1%81%D1%80%D0%BE%D1%87%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D0%B5%D0%B6%D0%B5%D0%B4%D0%BD%D0%B5%D0%B2%D0%BD%D1%8B%D1%85_%D1%86%D0%B5%D0%BD_%D0%BD%D0%B0_%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D1%8D%D0%BD%D0%B5%D1%80%D0%B3%D0%B8%D1%8E_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»