Эмпирическое распределение
Материал из MachineLearning.
Эмпирическая функция распределения — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.
Содержание |
Определения
Пусть задана случайная выборка наблюдений
Построим по выборке ступенчатую функцию
, возрастающую скачками величины
в точках
Построенная функция называется эмпирической функцией распределения.
Для задания значений в точках разрыва формально определим её так:
Замечание: при этом эмпирическая функция непрерывна справа.
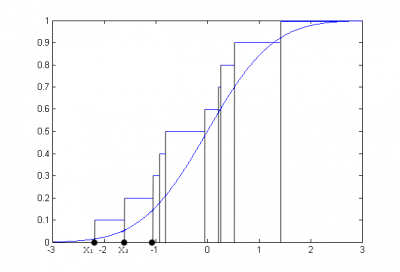
На рисунке представлена функция стандартного нормального распределения и эмпирическая функция распределения, построенная по выборке из 10 случайных наблюдений из стандартного нормального закона.
Свойства эмпирической функции распределения
Эмпирическое распределение для фиксированного 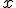
Поскольку случайная величина имеет распределение Бернулли с вероятностью успеха
(где
- теоретическая
функция распределения случайной величины
), а последовательность
- схема Бернулли с вероятностью успеха
, то по отношению к этой последовательности
есть частота попаданий левее x.
Математическое ожидание и дисперсия эмпирического распределения
Математическое ожидание эмпирической функции распределения
таким образом эмпирическое распределение является несмещённой оценкой теоретической функции распределения .
Дисперсия эмпирического распределения
Асимптотические свойства эмпирической функции распределения
- По усиленному закону больших чисел
сходится почти наверное к теоретической функции распределения