Распределение Фишера
Материал из MachineLearning.
Плотность вероятности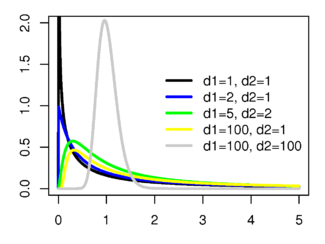
| |
Функция распределения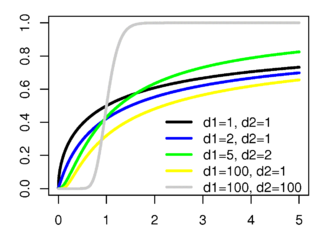
| |
| Параметры | |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | если |
| Коэффициент эксцесса | |
| Информационная энтропия | |
| Производящая функция моментов | ' |
| Характеристическая функция | |
Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.
Содержание |
Определение
Пусть — две независимые случайные величины, имеющие распределение хи-квадрат:
, где
. Тогда распределение случайной величины
-
,
называется распределением Фишера со степенями свободы и
. Пишут
.
Моменты
Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:
-
, если
,
-
, если
.
Свойства распределения Фишера
- Если
, то
-
.
- Распределение Фишера сходится к единице: если
, то
-
по распределению при
,
где — дельта-функция в единице, то есть распределение случайной величины-константы
.
Связь с другими распределениями
- Если
, то случайные величины
сходятся по распределению к
при
.

