Критерий хи-квадрат

Материал из MachineLearning.

(Различия между версиями)

Версия 15:07, 10 января 2009

Содержание

1 Определение
2 Проверка гипотезы
3 Пример 1
4 Сложная гипотеза
5 Пример 2
6 Проблемы
7 Литература
8 Ссылки

Критерий $\chi^2$ - статистический критерий для проверки гипотезы $H_0$ , что наблюдаемая случайная величина подчиняется некому теоретическому закону распределения.

Определение

Пусть дана случайная величина X .

Гипотеза $H_0$ : с. в. X подчиняется закону распределения $F(x)$ .

Для проверки гипотезы рассмотрим выборку, состоящую из n независимых наблюдений над с.в. X: $X^n = \left( x_1, \cdots x_n \right), \; x_i \in \left[ a, b \right], \; \forall i=1 \dots n$ . По выборке построим эмпирическое распределение $F^*(x)$ с.в X. Сравнение эмпирического $F^*(x)$ и теоретического распределения $F(x)$ (предполагаемого в гипотезе) производится с помощью специально подобранной функции — критерия согласия. Рассмотрим критерий согласия Пирсона (критерий $\chi^2$ ):

Гипотеза $H_0^*$ : Хⁿ порождается функцией $F^*(x)$ .

Разделим [a,b] на k непересекающихся интервалов $(a_i, b_i], \; i=1 \dots k$ ;

Пусть $n_j$ - количество наблюдений в j-м интервале: $n_j = \sum_{i=1}^n \left[ a_j <x_i \leq b_j \right]$ ;

$p_j = F(b_j)-F(a_j)$ - вероятность попадания наблюдения в j-ый интервал при выполнении гипотезы $H_0^*$ ;

$E_j = np_j$ - ожидаемое число попаданий в j-ый интервал;

Статистика: $\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-1}^2$ - Распределение хи-квадрат с k-1 степенью свободы.

Проверка гипотезы 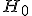$H_0$

Распределение хи-квадрат

В зависимости от значения критерия $\chi^2$ , гипотеза $H_0$ может приниматься, либо отвергаться:

$\chi^2_1 < \chi^2 < \chi^2_2$ , гипотеза $H_0$ выполняется.

$\chi^2 \leq \chi^2_1$ (попадает в левый "хвост" распределения). Следовательно, теоретические и практические значения очень близки. В таком случае, если, к примеру, происходит проверка генератора случайных чисел, который сгенерировал n чисел из отрезка [0,1] и гипотеза $H_0$ : выборка $X^n$ распределена равномерно на [0,1], тогда генератор нельзя называть случайным, т.к. выборка распределена слишком равномерно, но, несмотря на это, гипотеза $H_0$ выполняется.

$\chi^2 \geq \chi^2_2$ (попадает в правый "хвост" распределения) гипотеза $H_0$ отвергается.

Пример 1

Проверим гипотезу $H_0$ : если взять случайную выборку 100 человек из всего населения острова Кипр (генеральной совокупности), где количество мужчин и женщин примерно одинаково (встречаются с одинаковой частотой), то в наблюдаемой выборке отношение количества мужчин и женщин будет соотноситься с частотой как и во всей генеральной выборке(50/50). Пусть в наблюдаемой выборке 46 мужчин и 54 женщины, тогда число степеней свобод $k-1=2-1=1$ и

$\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j}= \frac{\left(46-50 \right)^2}{50}+\frac{\left(54-50 \right)^2}{50}=0,64$

Т.о. при уровне значимости $\alpha=0.05$ гипотеза $H_0$ выполняется (см. таблицу значений ф-ии $\chi^2_1$ ).

Сложная гипотеза

Гипотеза $H_0^*$ : Хⁿ порождается функцией $F(x,\theta),\; \theta \in R^d,\; \theta$ - неизвестный параметр. Найдем приближенное значение параметра $\hat{\theta}$ с помощью метода максимального правдоподобия, основанного на частотах (фиксируем интервалы $\left(a_j,b_j \right]$ для $j=1 \dots k$ ).

$n_j = \sum_{i=1}^n \left[ a_j <x_i \leq b_j \right]$ - число попаданий значений элементов выборки в j-ый интервал.

$p_j(\theta)=F(b_j,\theta)-F(a_j,\theta)$ ,

$\hat{\theta} = \arg \max_{\theta} \sum n_j \ln p_j(\theta)$

Теорема Фишера Для проверки сложной гипотезы критерий $\chi^2$ представляется в виде:

$\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-d-1}^2$ , где $E_j=n p_j\left(\hat{\theta}\right)$

Пример 2

Задача о бомбардировках Лондона [Лагутин, Т2]. Задача возникла в связи с бомбардировками Лондона во время Второй мировой войны. Для улучшения организации оборонительных мероприятий, необходимо было понять цель противника. Для этого территорию города условно разделили сеткой из 24-ёх горизонтальных и 24-ёх вертикальных линий на 576 равных участков. В течении некторого времени в центре организации обороны города собиралась информация о количестве попаданий снарядов в каждый из участков. В итоге были получены следующие данные:

Число попаданий	0	1	2	3	4	5	6	7
Количество участков	229	211	93	35	7	0	0	1

Гипотеза $H_0$ : стрельба случайна (нет "целевых" участков).

Закон редких событий (распределение Пуассона)

$P\{S=j\}=\frac{\lambda^j}{j!}e^{-\lambda}$ , S - число попаданий $\hat{\lambda}=0.924$

$\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j}= 32.6 \sim \chi_{8-1-1}^2$

Тогда при уровне значимости $\alpha=0.05$ гипотеза $H_0$ не выполняется (см. таблицу значений ф-ии $\chi^2_6$ ).

Объединим события (4,5,6,7) с малой частотой попаданий в одно, тогда имеем:

Число попаданий	0	1	2	3	4-7
Количество участков	229	211	93	35	8

$\chi^2 = 1.05 \sim \chi_{5-1-1}^2$ ,

тогда при уровне значимости $\alpha=0.05$ гипотеза $H_0$ верна.

Проблемы

Критерий $\chi^2$ ошибается на выборках с низкочастотными (редкими) событиями. Решить эту проблему можно отбросив низкочастотные события, либо объединив их с другими событиями. Этот способ называется коррекцией Йетса (Yates' correction).

Литература

Лапач С. Н. , Чубенко А. В., Бабич П. Н. Статистика в науке и бизнесе. (стр. 204,316) — Киев: Морион, 2002.

Лагутин М. Б. Наглядная математическая статистика. (Том 2, стр. 174) — М.: П-центр, 2003.

Кулаичев А. П. Методы и средства комплексного анализа данных. (стр. 162) — М.: Форум–Инфра-М, 2006.

Ссылки

[Критерий хи-квадрат (en.wiki)]

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82»

Категории: Незавершённые статьи | Прикладная статистика | Энциклопедия анализа данных

@@ Строка 57: / Строка 57: @@
 == Пример 2 ==
+'''Задача о бомбардировках Лондона [Лагутин, Т2].'''
+Задача возникла в связи с бомбардировками Лондона во время Второй мировой войны. Для улучшения организации оборонительных мероприятий, необходимо было понять цель противника. Для этого территорию города условно разделили сеткой из 24-ёх горизонтальных и 24-ёх вертикальных линий на 576 равных участков. В течении некторого времени в центре организации обороны города собиралась информация о количестве попаданий снарядов в каждый из участков. В итоге были получены следующие данные:
-Пусть есть квадрат на местности, разделенный сеткой из 24-ёх горизонтальных и 24-ёх вертикальных линий на 576 равных участков. По квадрату производится артиллерийский обстрел. Подсчитывается количество попаданий снарядов в каждый из участков. Получены следующие данные: 0 попаданий - 229 участков, 1 попадание - 211 участок, 2 - 93, 3 - 35, 4 - 7, 5 и 6 - 0, 7 - 1 попадание. Гипотеза <tex>H_0</tex>: стрельба случайна (нет "целевых" участков).
+{| border=1 cellpadding="6" cellspacing="0"
+|- align="center"
+! Число попаданий
+|0 || 1 || 2 || 3 || 4 || 5 || 6 || 7
+|- align="center"
+! Количество участков
+|229 || 211 || 93 || 35 || 7 || 0 || 0 || 1
+|}
+Гипотеза <tex>H_0</tex>: стрельба случайна (нет "целевых" участков).
 Закон редких событий ([[Распределение Пуассона|распределение Пуассона]])
-<tex>P{S=j}=\frac{\lambda^j}{j!}e^{-\lambda}</tex>, S - число попаданий <tex>\hat{\lambda}=0.924</tex>
+<tex>P\{S=j\}=\frac{\lambda^j}{j!}e^{-\lambda}</tex>, S - число попаданий  <tex>\hat{\lambda}=0.924</tex>
 <tex>\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j}= 32.6 \sim \chi_{8-1-1}^2</tex>
-Тогда при уровне значимости <tex>\alpha=0.05</tex> гипотеза <tex>H_0</tex> не выполняется (см. таблицу значений ф-ии <tex>\chi^2_6</tex>).
+Тогда при уровне значимости <tex>\alpha=0.05</tex> гипотеза <tex>H_0</tex> не выполняется (см. [http://www.statsoft.ru/home/textbook/modules/sttable.html таблицу значений ф-ии <tex>\chi^2_6</tex>]).
 Объединим события (4,5,6,7) с малой частотой попаданий в одно, тогда имеем:
-попадание - 211 участок, 2 - 93, 3 - 35, {4,5,6,7} - 8.
+{| border=1 cellpadding="6" cellspacing="0"
+|- align="center"
+! Число попаданий
+|0 || 1 || 2 || 3 || 4-7
+|- align="center"
+! Количество участков
+|229 || 211 || 93 || 35 || 8
+|}
-<tex>\chi^2 = 1.05 \sim \chi_{5-1-1}^2</tex>
+<tex>\chi^2 = 1.05 \sim \chi_{5-1-1}^2</tex>,
 тогда при уровне значимости <tex>\alpha=0.05</tex> гипотеза <tex>H_0</tex> верна.