Коэффициент детерминации

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м
Строка 1: Строка 1:
-
'''Коэффициентом детерминации''', <tex>R^2</tex>, называется величина, показывающая, какая доля [[дисперсия|дисперсии]] выборки определяется параметрами выбранной модели.
+
'''Коэффициент детерминации''' ('''<tex>R^2</tex>''' - ''R-квадрат'') — это доля [[дисперсия случайной величины|дисперсии]] зависимой переменной, объясняемая рассматриваемой моделью. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по признакам дисперсии зависимой переменной) в дисперсии зависимой переменной. В случае линейной зависимости <tex>R^2</tex> является квадратом так называемого [[Множественная корреляция|множественного коэффициента корреляции]] между зависимой переменной и объясняющими переменными. В частности, для модели линейной регрессии с одним признаком <tex>x</tex> коэффициент детерминации равен квадрату обычного коэффициента корреляции между <tex>y</tex> и <tex>x</tex>.
-
== Определение ==
+
=Определение и формула=
-
Существует несколько альтернативных определений '''коэффициента детерминации''', однако в случае [[Регрессионный анализ|линейной регрессии]] все они эквивалентны: <tex>R^2</tex> тогда равен квадрату [[коэффициент корреляции|коэффициента корреляции]].
+
Истинный коэффициент детерминации модели зависимости случайной величины <tex>y</tex> от признаков <tex>x</tex> определяется следующим образом:
-
Пусть выборка имеет значения <tex>y_i</tex>, и ей соответствуют модельные данные <tex>f_i</tex>; <tex>\bar{y}</tex> и <tex>\bar{f}</tex> - средние значения наблюдаемых и модельных данных. Тогда введем следующие обозначения:
+
: <tex>R^2 =1-\frac {V(y|x)}{V(y)}=1-\frac {\sigma^2}{\sigma^2_y},</tex>
-
<tex>SS_{\rm tot}=\sum_i (y_i-\bar{y})^2,</tex> общая сумма квадратов отклонения (пропорциональная дисперсии);
+
где <tex>V(y|x)=\sigma^2</tex> — условная (по признакам <tex>x</tex>) дисперсия зависимой переменной (дисперсия случайной ошибки модели).
-
<tex>SS_{\rm reg}=\sum_i ({f_i}-\bar{f})^2,</tex> регрессионная сумма квадратов отклонений (объяснимая моделью);
+
В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):
 +
: <tex>R^2 =1-\frac {\hat{\sigma}^2}{\hat{\sigma}^2_y}=1-\frac {ESS/n}{TSS/n}=1-\frac {ESS} {TSS},</tex>
 +
где
 +
:<tex>ESS=\sum^n_{t=1}e^2_t=\sum^n_{t=1} (y_t-\hat y_t)^2</tex> — сумма квадратов регрессионных остатков,
 +
:<tex>TSS=\sum^n_{t=1} (y_t-v)^2=n \hat \sigma^2_y</tex> — общая дисперсия,
 +
:<tex>y_t,\hat y_t</tex> — соответственно, фактические и расчетные значения объясняемой переменной,
 +
:<tex>\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i </tex> — выборочное вреднее.
-
<tex>SS_{\rm err}=\sum_i (y_i - {f}_i)^2\,</tex>, сумма квадратов ошибок.
+
В случае [[линейная регрессия|линейной регрессии]] ''с константой'' <tex>TSS=RSS+ESS</tex>, где <tex>RSS=\sum^n_{t=1} (\hat y_t-\bar{y})^2</tex> — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае. ''Коэффициент детерминации — это доля объяснённой дисперсии в общей'':
 +
:<tex>R^2=\frac {RSS} {TSS}</tex>.
-
Общее определение коэффициента детерминированности:
+
Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.
-
<tex>R^2 \equiv 1 - {SS_{\rm err}\over SS_{\rm tot}}.\,</tex>
+
=Интерпретация=
 +
# Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Равенство коэффициента детерминации единице означает, что объясняемая переменная в точности описывается рассматриваемой моделью.
 +
# При отсутствии статистической связи между объясняемой переменной и признаками статистика <tex>nR^2</tex> для [[линейная регрессия|линейной регрессии]] имеет асимптотическое распределение <tex>\chi^2(k-1)</tex>, где <tex>k-1</tex> — число признаков в модели. В случае линейной регрессии с независимыми одинаково распределёнными нормальными случайными ошибками статистика <tex>F=\frac {R^2/(k-1)}{(1-R^2)/(n-k)}</tex> имеет точное (для выборок любого объёма) [[распределение Фишера]] <tex>F(k-1,n-k)</tex>. Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.
-
Дробь <tex>{SS_{\rm err}\over SS_{\rm tot}}</tex> показывает отношение не объясненных моделью вариаций к общим вариациям, так что введенное таким образом определение ясно отражает суть понятия '''коэффициент детерминации'''.
+
= Недостатки <tex>R^2</tex> и альтернативные показатели=
-
== Интерпретация ==
+
Основная проблема применения (выборочного) <tex>R^2</tex> заключается в том, что его значение увеличивается (''не'' уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют. Поэтому сравнение моделей с разным количеством признаков с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.
-
<tex>R^2</tex> содержит информацию о том, насколько хорошо модель подходит под исходные данные. Например, в случае решения задачи [[регрессия|регрессии]] коэффициент детерминации покажет, насколько график модельных значений совпадает с графиком наблюдаемых значений: если <tex>R^2 = 1</tex>, то эти графики совпадают. Однако само по себе значение '''коэффициента детерминированности''' не может свидетельствовать о том, что модель выбрана правильно.
+
== Скорректированный (adjusted) <tex>R^2</tex> ==
 +
Для того, чтобы была возможность сравнивать модели с разным числом признаков так, чтобы число регрессоров (признаков) не влияло на статистику <tex>R^2</tex> обычно используется ''скорректированный коэффициент детерминации'', в котором используются несмещённые оценки дисперсий:
 +
:<tex>R_{adj}^2 =1-\frac {s^2}{s^2_y}=1-\frac {ESS/(n-k)}{TSS/(n-1)}=1-(1- R^2) {(n-1) \over (n-k)}\leq R^2,</tex>
 +
 
 +
который даёт штраф за дополнительно включённые признаки, где <tex>n</tex> — количество наблюдений, а <tex>k</tex> — количество параметров.
 +
 
 +
Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве признаков), поэтому интерпретировать его как долю объясняемой дисперсии уже нельзя. Тем не менее, применение показателя в сравнении вполне обоснованно.
 +
 
 +
Для моделей с одинаковой зависимой переменной и одинаковым объемом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии <tex>s^2=ESS/(n-k)</tex> или стандартной ошибки модели <tex>s</tex>.
 +
 
 +
== Обобщённый (extended) <tex>R^2</tex>==
 +
В случае отсутствия в линейной множественной МНК регрессии константы свойства коэффициента детерминации могут нарушаться для конкретной [[Случайный эксперимент|реализации]]. Поэтому модели регрессии со свободным членом и без него нельзя сравнивать по критерию <tex>R^2</tex>. Эта проблема решается с помощью построения обобщённого коэффициента детерминации <tex>R_{ext}^2</tex>, который совпадает с исходным для случая МНК регрессии со свободным членом. Суть этого метода заключается рассмотрении проекции единичного вектора на плоскость объясняющих переменных.
 +
 
 +
Для случая регрессии без свободного члена:
 +
:<tex>R_{ext}^2 = 1- {Y'*(I-P(X))*Y \over Y'*(I-\pi(X))*Y},</tex>
 +
где <tex>X</tex> — матрица <tex>n\times k</tex> значений признаков, <tex>P(X) = X*(X'*X)^{-1}*X'</tex> — проектор на плоскость <tex>X</tex>, <tex>\pi(X) = {P(X)*i_n*i_n'*P(X) \over i_n'*P(X)*i_n}</tex>, <tex>i_n</tex> — единичный вектор <tex>n\times 1</tex>.
 +
 
 +
При некоторой модификации <tex>R_{ext}^2</tex> также подходит для сравнения между собой регрессионных моделей, построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).
== Ссылки ==
== Ссылки ==

Версия 22:52, 24 декабря 2012

Коэффициент детерминации (R^2 - R-квадрат) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по признакам дисперсии зависимой переменной) в дисперсии зависимой переменной. В случае линейной зависимости R^2 является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными. В частности, для модели линейной регрессии с одним признаком x коэффициент детерминации равен квадрату обычного коэффициента корреляции между y и x.

Содержание

Определение и формула

Истинный коэффициент детерминации модели зависимости случайной величины y от признаков x определяется следующим образом:

R^2 =1-\frac {V(y|x)}{V(y)}=1-\frac {\sigma^2}{\sigma^2_y},

где V(y|x)=\sigma^2 — условная (по признакам x) дисперсия зависимой переменной (дисперсия случайной ошибки модели).

В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):

R^2 =1-\frac {\hat{\sigma}^2}{\hat{\sigma}^2_y}=1-\frac {ESS/n}{TSS/n}=1-\frac {ESS} {TSS},

где

ESS=\sum^n_{t=1}e^2_t=\sum^n_{t=1} (y_t-\hat y_t)^2 — сумма квадратов регрессионных остатков,
TSS=\sum^n_{t=1} (y_t-v)^2=n \hat \sigma^2_y — общая дисперсия,
y_t,\hat y_t — соответственно, фактические и расчетные значения объясняемой переменной,
\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i — выборочное вреднее.

В случае линейной регрессии с константой TSS=RSS+ESS, где RSS=\sum^n_{t=1} (\hat y_t-\bar{y})^2 — объяснённая сумма квадратов, поэтому получаем более простое определение в этом случае. Коэффициент детерминации — это доля объяснённой дисперсии в общей:

R^2=\frac {RSS} {TSS}.

Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.

Интерпретация

  1. Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Равенство коэффициента детерминации единице означает, что объясняемая переменная в точности описывается рассматриваемой моделью.
  2. При отсутствии статистической связи между объясняемой переменной и признаками статистика nR^2 для линейной регрессии имеет асимптотическое распределение \chi^2(k-1), где k-1 — число признаков в модели. В случае линейной регрессии с независимыми одинаково распределёнными нормальными случайными ошибками статистика F=\frac {R^2/(k-1)}{(1-R^2)/(n-k)} имеет точное (для выборок любого объёма) распределение Фишера F(k-1,n-k). Информация о распределении этих величин позволяет проверить статистическую значимость регрессионной модели исходя из значения коэффициента детерминации. Фактически в этих тестах проверяется гипотеза о равенстве истинного коэффициента детерминации нулю.

Недостатки 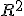R^2 и альтернативные показатели

Основная проблема применения (выборочного) R^2 заключается в том, что его значение увеличивается (не уменьшается) от добавления в модель новых переменных, даже если эти переменные никакого отношения к объясняемой переменной не имеют. Поэтому сравнение моделей с разным количеством признаков с помощью коэффициента детерминации, вообще говоря, некорректно. Для этих целей можно использовать альтернативные показатели.

Скорректированный (adjusted) 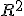R^2

Для того, чтобы была возможность сравнивать модели с разным числом признаков так, чтобы число регрессоров (признаков) не влияло на статистику R^2 обычно используется скорректированный коэффициент детерминации, в котором используются несмещённые оценки дисперсий:

R_{adj}^2 =1-\frac {s^2}{s^2_y}=1-\frac {ESS/(n-k)}{TSS/(n-1)}=1-(1- R^2) {(n-1) \over (n-k)}\leq R^2,

который даёт штраф за дополнительно включённые признаки, где n — количество наблюдений, а k — количество параметров.

Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве признаков), поэтому интерпретировать его как долю объясняемой дисперсии уже нельзя. Тем не менее, применение показателя в сравнении вполне обоснованно.

Для моделей с одинаковой зависимой переменной и одинаковым объемом выборки сравнение моделей с помощью скорректированного коэффициента детерминации эквивалентно их сравнению с помощью остаточной дисперсии s^2=ESS/(n-k) или стандартной ошибки модели s.

Обобщённый (extended) 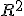R^2

В случае отсутствия в линейной множественной МНК регрессии константы свойства коэффициента детерминации могут нарушаться для конкретной реализации. Поэтому модели регрессии со свободным членом и без него нельзя сравнивать по критерию R^2. Эта проблема решается с помощью построения обобщённого коэффициента детерминации R_{ext}^2, который совпадает с исходным для случая МНК регрессии со свободным членом. Суть этого метода заключается рассмотрении проекции единичного вектора на плоскость объясняющих переменных.

Для случая регрессии без свободного члена:

R_{ext}^2 = 1- {Y'*(I-P(X))*Y \over Y'*(I-\pi(X))*Y},

где X — матрица n\times k значений признаков, P(X) = X*(X'*X)^{-1}*X' — проектор на плоскость X, \pi(X) = {P(X)*i_n*i_n'*P(X) \over i_n'*P(X)*i_n}, i_n — единичный вектор n\times 1.

При некоторой модификации R_{ext}^2 также подходит для сравнения между собой регрессионных моделей, построенных с помощью: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК).

Ссылки

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%B4%D0%B5%D1%82%D0%B5%D1%80%D0%BC%D0%B8%D0%BD%D0%B0%D1%86%D0%B8%D0%B8»
Личные инструменты