Исследование скорости сходимости параметров и гиперпараметров (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 10:56, 12 марта 2012

Содержание

1 Постановка задачи
2 Алгоритм настройки регрессионной модели (двухуровневый байесовский вывод)
- 2.1 Описание метода
- 2.2 Алгоритм
3 Вычислительный эксперимент
- 3.1 Литература
- 3.2 Исходный код

Для фиксированной регрессионной модели исследуется скорость сходимости параметров и гиперпараметров при ее настройке через двухуровневый байесовский вывод.

Постановка задачи

Рассмотрим следующую модель регрессии, описывающую связь между свободной и зависимой переменными:

$\mathbf{y} = f(\mathbf{x}, \mathbf{w}) + \mathbf{\varepsilon}$

Пусть случайная величина $\mathbf{\varepsilon}$ имеет нормальное распределение $\mathbf{\varepsilon} \in N(0, \sigma^2)$ . При этом будем обозначать $\mathbf{\beta}=\frac1{\sigma^2}$ .

Вектор $\mathbf{w}$ называется параметрами модели и рассматривается как многомерная случайная величина. Пусть плотность распределения параметров имеет вид многомерного нормального распределения $N(\mathbf{0}, A)$ с матрицей ковариации $A$ . В данном примере будут рассматриваться 2 случая: $A^{-1}=diag(\alpha_1, \alpha_2, \dots, \alpha_W)=diag(\mathbf{\alpha})$ , где $W$ - число параметров модели, и $A^{-1}=\alpha I_W$ , где $I_W$ - единичная матрица размерности $W$ .

Величины $\mathbf{\beta}$ и $\mathbf{\alpha}$ называются гиперпараметрами модели.

Для нескольких фиксированных функций $f$ , задающих модель, через двухуровневый байесовский вывод происходит настройка параметров и гиперпараметров. Требуется проанализировать изменение параметров и гиперпараметров по мере настройки.

Алгоритм настройки регрессионной модели (двухуровневый байесовский вывод)

Настройка модели происходит через двухуровневый байесовский вывод.

Описание метода

Т.к. $\mathbf{\varepsilon} \in N(0, \beta^{-2})$ , то для фиксированной модели f плотность вероятности появления данных

$P(y|\,\mathbf{x},\mathbf{w}, \beta, f)\equiv P(D|\, \mathbf{w}, \beta, f)=(\frac{2 \pi}\beta)^{-\frac{N}2}\, \exp(-\beta E_D)$ ,

где

$E_D = \frac12 \sum_{n=1}^N (f(\mathbf{w},\mathbf{x}_n)-y_n)^2$

Т.к. $\mathbf{w} \in N(\mathbf{0}, A)$ , то

$P(\mathbf{w}|\, A, f)=\frac{1}{(2 \pi)^{\frac{W}2}{|A|}^{\frac12}}\,\exp(-E_W)$ ,

где

$E_W = \frac12 \mathbf{w}^T A^{-1}\mathbf{w}$

Тогда, если обозначить $S(\mathbf{w})=E_W + \beta E_D = \frac12 \mathbf{w}^T A^{-1}\mathbf{w} + \beta E_D$ , то

$P(\mathbf{w}|\,D, A, \beta, f)= \frac{P(D|\, \mathbf{w}, \beta, f) P(\mathbf{w}|\, A, f)}{P(D|\, A, \beta, f)} \propto \exp(-S(\mathbf{w}))$

Таким образом, минимизация $S(\mathbf{w})$ по $\mathbf{w}$ дает максимум априорной плотности распределения параметров $\mathbf{w}$ на выборке $D$ . Минимизация осуществляется алгоритмом Левенберга-Марквардта.

Считая, что в точке минимума $\mathbf{w}^*$ функционал $S(\mathbf{w})$ представим в виде:

$S(\mathbf{w}) = S(\mathbf{w}^*) + \frac12 \Delta\mathbf{w}^T H \Delta\mathbf{w}$ , где $H=-\nabla\nabla S(w)|_{w=w^*}$ - гессиан функции ошибок,

получаем, что логарифм функции правдоподобия равен

$ln P(D|\,\mathbf{\alpha}, \mathbf{\beta})= - \frac12 ln|A| - \frac{N}2 ln 2\pi + \frac{N}2 ln \beta - \beta E_D - E_W -\frac12 ln|H|$

Гиперпараметры $\mathbf{\beta}$ и $\mathbf{\alpha}$ находятся итерационно из условия максимизации полученной функции правдоподобия:

При $A^{-1}=diag(\mathbf{\alpha})=diag(\alpha_1, \alpha_2, \dots, \alpha_W)$

$\alpha_i= \frac{-\lambda_i + \sqrt{\lambda_i^2 + 4 \frac{\lambda_i}{w_i^2}}}2$ , где $\lambda_i$ - собственные числа матрицы $H_D$ - части Гессиана, не зависящей от $A$ .

$\beta= \frac{N-\gamma}{2 E_D}$ , где $\gamma=\sum^W_{j=1}\frac{\lambda_j}{\lambda_j+a_j}$

При $A^{-1}=\alpha I_W$

$\alpha = \frac{W-\delta}{\mathbf{w}^T \mathbf{w}}$ , где $\delta=\sum^W_{j=1}\frac{\alpha}{\lambda_j+\alpha}$

$\beta= \frac{N-\gamma}{2 E_D}$ , где $\gamma=\sum^W_{j=1}\frac{\lambda_j}{\lambda_j+\alpha}$

Алгоритм

1) Задаем начальные значения $\mathbf{w_0}$ , $\mathbf{\alpha_0}$ и $\mathbf{\beta_0}$

2) Ищем локальный минимум функции ошибки $S(\mathbf{w})$ по $\mathbf{w}$

3) Ищем локальный максимум функции правдоподобия гиперпараметров $P(D|\,\mathbf{\alpha}, \mathbf{\beta})$ по $\mathbf{\alpha}, \mathbf{\beta}$

4) Повторяем шаги 2 и 3 до сходимости функционала $S(\mathbf{w})$

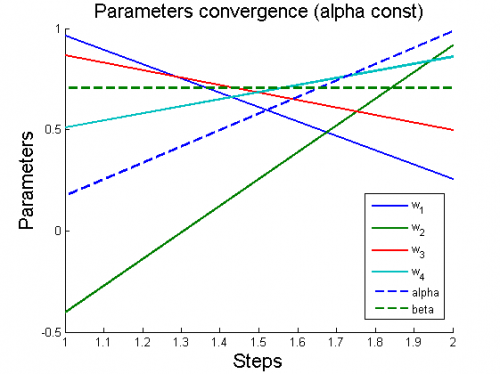
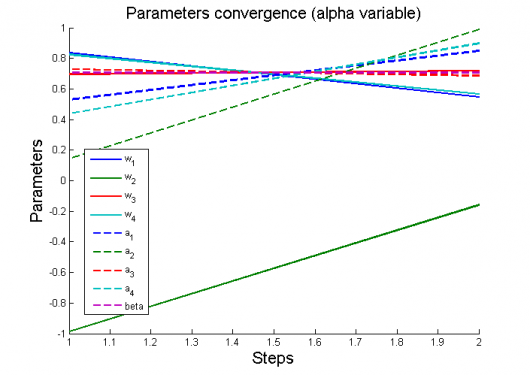
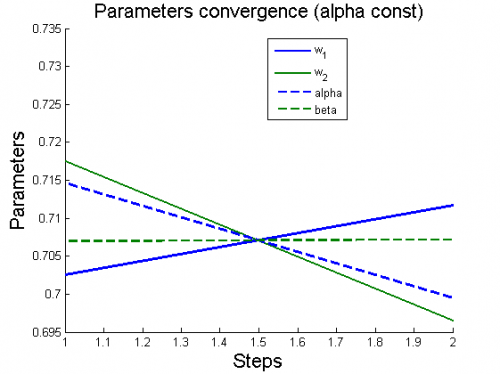
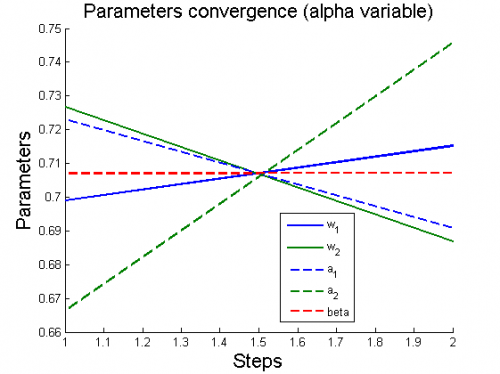
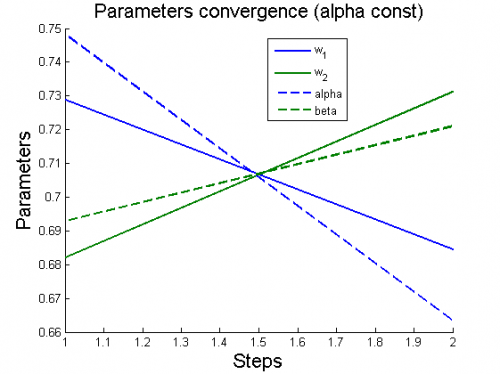
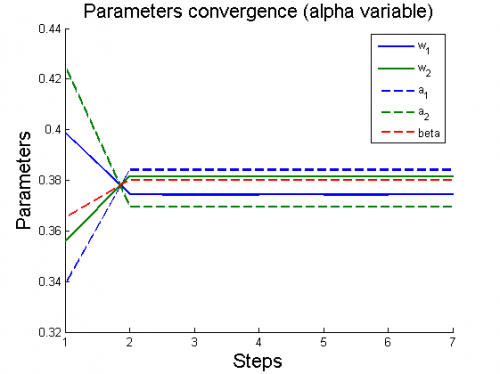
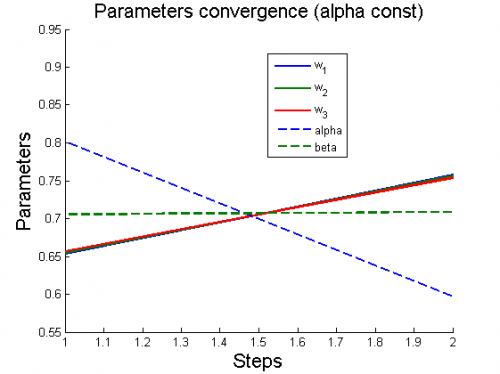
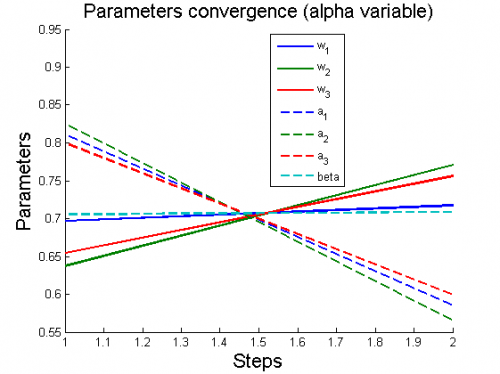
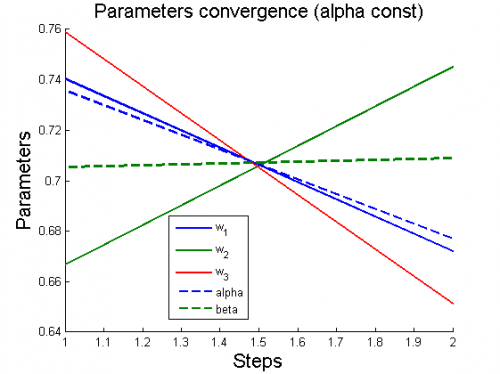
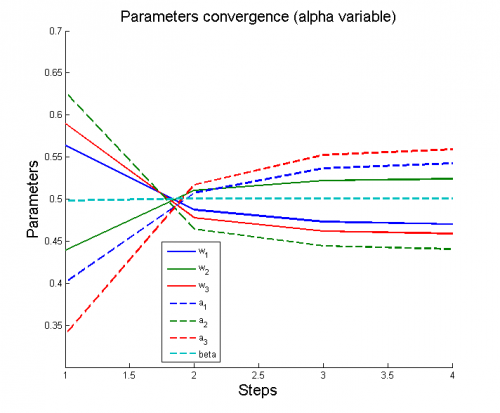
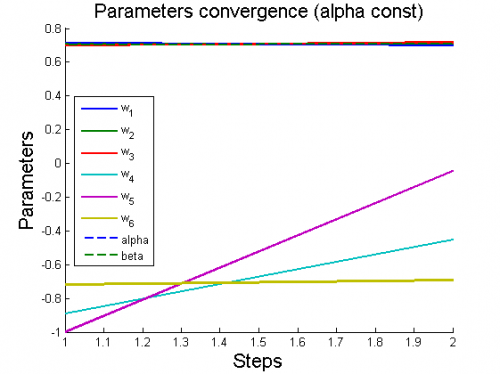
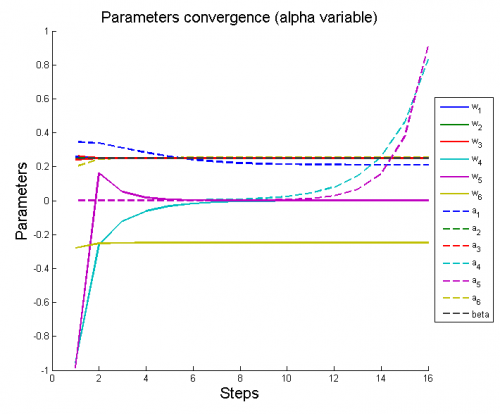
Вычислительный эксперимент

Эксперименты проводятся на 6 моделях, для каждой из которых рассматриваются 2 случая: $A^{-1}=diag(\mathbf{\alpha})$ (alpha variable) и $A^{-1}=\alpha I_W$ (alpha constant).

Для каждого случая проводится настройка модели по описанному алгоритму. Затем строятся графики изменения параметров и гиперпараметров по шагам алгоритма (величины параметров и гиперпараметров нормированы).

Рассматриваемые модели:

1) модель полиномиальной регрессии $y=\sum_{i=1}^4 w_i x^{i-1}$

2) модель $y = w_1 + w_2\, ln x$

3) модель $y = w_1 + \frac{w_2}{x}$

4) модель $y = w_1 + w_2\, e^{-w_3x}$

5) модель трехпараметрического распределения Вейбулла $y=w_1 w_2 x^{w_2-1}\exp(-w_1(x-w_3)^{w_2})$

6) модель с тригонометрическими функциями $y=a_0+\sum_{i=1}^n\bigl(a_i\cos(i\omega{x})+b_i\sin(i\omega{x})\bigr)$

Код требует дополнительной проверки: очень быстрая сходимость в большинстве вариантов.

Литература

Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Стрижов В. В., Сологуб Р.А. Алгоритм выбора нелинейных регрессионных моделей с анализом гиперпараметров. Всероссийская конференция «Математические методы распознавания образов» (ММРО-14). 2009. стр. 184-187

Исходный код

Sintsova2010Bayesian

Данная статья была создана в рамках учебного задания.

Студент: Участник:Валентина Синцова

Преподаватель: В.В.Стрижов

Срок: 24 декабря 2010

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%98%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D0%B8_%D1%81%D1%85%D0%BE%D0%B4%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B8_%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%BE%D0%B2_%D0%B8_%D0%B3%D0%B8%D0%BF%D0%B5%D1%80%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%BE%D0%B2_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категория: Практика и вычислительные эксперименты

@@ Строка 120: / Строка 120: @@
 == Исходный код ==
-[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/BayesianConvergence/  SourceForge, BayesianConvergence]
+[https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Sintsova2010Bayesian/  Sintsova2010Bayesian]
 {{ЗаданиеВыполнено|Валентина Синцова|В.В.Стрижов|24 декабря 2010||Strijov}}
 [[Категория:Практика и вычислительные эксперименты]]

Исследование скорости сходимости параметров и гиперпараметров (пример)

Материал из MachineLearning.

Версия 10:56, 12 марта 2012

Содержание

Постановка задачи

Алгоритм настройки регрессионной модели (двухуровневый байесовский вывод)

Описание метода

Алгоритм

Вычислительный эксперимент

Литература

Исходный код

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты