Статистический анализ данных (курс лекций, К.В.Воронцов)/2011

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м (Новая: {{TOCright}} = Задание 1. Исследование свойств одномерных статистических критериев на модельных данных = Не...)
м
Строка 33: Строка 33:
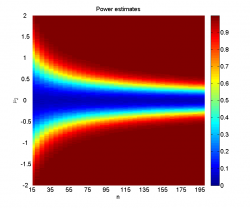
Изображение:3000_pow.png|Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов (<tex>\alpha=0.05</tex>).
Изображение:3000_pow.png|Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов (<tex>\alpha=0.05</tex>).
</gallery>
</gallery>
-
Во-первых, заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, поэтому для
+
 
 +
Во-первых, заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, поэтому и необходимо усреднение по большому числу экспериментов.
 +
 
Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Наоборот, когда разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а средний достигаемый уровень значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на <tex>[0,1]</tex>.
Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Наоборот, когда разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а средний достигаемый уровень значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на <tex>[0,1]</tex>.
Строка 42: Строка 44:
</gallery>
</gallery>
-
Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.
+
Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.
Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.
Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.
 +
 +
== Задания==
 +
=== Анализ чувствительности критериев к редактированию выборки===
 +
Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность указанного критерия к редактированию выборки, построить графики, сделать выводы.
 +
* Двухвыборочный [[критерий Стьюдента]] для связных выборок.
 +
* [[Критерий Уилкоксона-Манна-Уитни]] для независимых выборок.
 +
* [[Критерий Фишера]] для проверки равенства дисперсий.
 +
 +
=== Устойчивость критериев к нарушению предположений ===
 +
=== Анализ поведения схожих критериев ===

Версия 21:55, 29 сентября 2011

Содержание

Задание 1. Исследование свойств одномерных статистических критериев на модельных данных

Необходимо провести исследование одного или нескольких классических критериев проверки статистических гипотез. Интерес представляет поведение достигаемого уровня значимости (p-value) как функции размера выборок и параметров распределения. В соответствии с индивидуальными параметрами задания необходимо указанным способом сгенерировать одну или несколько выборок из заданного распределения, выполнить проверку гипотезы при помощи соответствующего критерия, а затем многократно повторить эту процедуру для различных значений параметров. По результатам расчётов необходимо построить требуемые в задании графики, среди которых могут быть следующие:

  1. график зависимости достигаемого уровня значимости от значений параметров при однократном проведении эксперимента;
  2. график зависимости достигаемого уровня значимости одного или двух критериев от значений параметров, усреднённого по большому количеству повторений эксперимента (например, по 1000 повторений);
  3. график с эмпирическими оценками мощности одного или двух критериев для разных значений параметров.

В качестве оценки мощности принимается доля отвержений нулевой гипотезы среди всех проверок. То есть, если эксперимент повторялся k раз для каждого набора значений параметра, и в m из k случаев гипотеза была отвергнута на некотором фиксированном уровне значимости \alpha (примем \alpha=0.05), оценкой мощности будет отношение m/k.

Необходимо сдать: выполненный в LaTex или Microsoft Word отчёт с описанием алгоритма, построенными графиками и выводами (объяснение полученных результатов моделирования, границы применимости критерия и т.д.), а также *.m-файл или R-скрипт, при запуске которого на экран выводятся графики, соответствующие имеющимся в отчёте.

Задание принимается до первого ноября.

Пример задания

Исследуем чувствительность классического двухвыборочного критерия Стьюдента для проверки гипотезы однородности против альтернативы сдвига при зашумлении выборок наблюдениями, взятыми из равномерного распределения.

x^n \sim 0.9\cdot N(\mu_1,1)+ 0.1\cdot U\left[-5+\mu_1,5+\mu_1\right] — выборка длины n из смеси стандартного нормального N(\mu_1,1) и равномерного U\left[-5+\mu_1,5+\mu_1\right] распределений с весами 0.9 и 0.1 соответственно (при генерации выборки используется случайный датчик — если его значение не превосходит 0.9, то добавляем в выборку элемент, взятый из нормального распределения, иначе — элемент, взятый из равномерного).

y^n \sim 0.9\cdot N(\mu_2,1)+ 0.1\cdot U\left[-5+\mu_2,5+\mu_2\right] — аналогичная выборка.

H_0\,:\; \mu_1=\mu_2,

H_1\,:\; \mu_1\neq\mu_2.

\mu_1=0, \;\; \mu_2=-2\,:\,0.01\,:\,2, \;\; n=15\,:\,5\,:\,200.

При каждом значении \mu_2 выборки для разных значений n генерируются независимо.

Значения достигаемого уровня значимости при однократной генерации выборок.

Значения достигаемого уровня значимости, усрёднённые по 3000 экспериментам.

Значения эмпирических оценок мощности критерия при проведении 3000 экспериментов (\alpha=0.05).

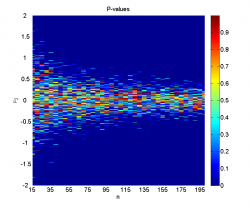
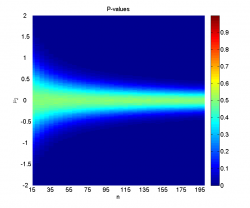
Во-первых, заметим, что однократная генерация выборок даёт достаточно нестабильные результаты, поэтому и необходимо усреднение по большому числу экспериментов.

Видно, что при достаточно большой разнице между средними и большом размере выборок наличие шума не мешает уверенно отклонять гипотезу однородности. Наоборот, когда разница между средними невелика (меньше 0.2-0.5 в зависимости от размера выборок), мощность близка к нулю, а средний достигаемый уровень значимости колеблется около 0.5, что логично, так как его распределение при справедливости нулевой гипотезы равномерно на [0,1].

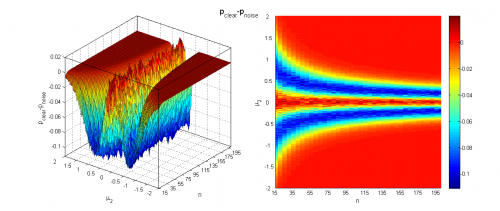
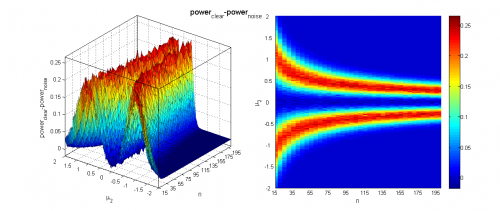
Чтобы оценить вклад зашумления выборок, оценим при всех значениях параметра мощность критерия и средний достигаемый уровень значимости на аналогичных выборках без шума и сравним результаты.

Разность средних достигаемых уровней значимости на выборках без шума и с шумом.

Разность эмпирических оценок мощности на выборках без шума и с шумом.

Видно, что наличие шума всё меньше влияет на работу критерия с ростом объёма выборок и разницы между их средними. Тем не менее, в некоторых областях изменения параметров потеря мощности из-за 10% зашумления может составлять до 20%, а средний достигаемый уровень значимости может быть выше на 0.1.

Отметим, что приведённые количественные выводы справедливы только для шума рассматриваемой структуры.

Задания

Анализ чувствительности критериев к редактированию выборки

Известно, что исключение из выборки определённых наблюдений зачастую может достаточно сильно повлиять на результат анализа. Необходимо исследовать чувствительность указанного критерия к редактированию выборки, построить графики, сделать выводы.

Устойчивость критериев к нарушению предположений

Анализ поведения схожих критериев

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A1%D1%82%D0%B0%D1%82%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%28%D0%BA%D1%83%D1%80%D1%81_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D0%B9%2C_%D0%9A.%D0%92.%D0%92%D0%BE%D1%80%D0%BE%D0%BD%D1%86%D0%BE%D0%B2%29/2011»