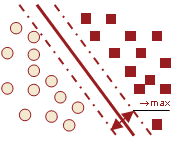
SVM для линейно разделимой выборки (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Постановка задачи линейной классификации)
Строка 1: Строка 1:
[[Изображение:SVMsample.gif|thumb]]
[[Изображение:SVMsample.gif|thumb]]
-
'''[[Машина опорных векторов]] (SVM — support vector machines)''' — группа алгоритмов классификации, основанных на обучении с учителем, использующих линейное разделение объектов в пространстве признаков с помощью гиперплоскости. Метод применяется для решения задачи бинарной классификации. Основной проблемой метода является выбор оптимальной гиперплоскости, которая позволяет разделить классы с максимальной точностью. Для этого разделяющая гиперплоскость должна быть выбрана таким образом, чтобы расстояние междуближайшими точками, расположенными по разные стороны от нее, было бы максимальным. Данное расстояние называется зазором (margin), а сами точки – оперными векторами (support vectors). Тогда разделяющая гиперплоскость должна быть выбрана таким образом, чтобы максимизировать зазор, что обеспечит более уверенное разделение классов.
+
'''[[Машина опорных векторов]] (SVM — support vector machines)''' — группа алгоритмов классификации, основанных на обучении с учителем, использующих линейное разделение объектов в пространстве признаков с помощью гиперплоскости. Метод применяется для решения задачи бинарной классификации. Основной проблемой метода является выбор оптимальной гиперплоскости, которая позволяет разделить классы с максимальной точностью. Для этого разделяющая гиперплоскость должна быть выбрана таким образом, чтобы расстояние междуближайшими точками, расположенными по разные стороны от нее, было бы максимальным. Данное расстояние называется зазором (margin), а сами точки – опорными векторами (support vectors). Тогда разделяющая гиперплоскость должна быть выбрана таким образом, чтобы максимизировать зазор, что обеспечит более уверенное разделение классов.

Версия 16:08, 28 апреля 2010

Машина опорных векторов (SVM — support vector machines) — группа алгоритмов классификации, основанных на обучении с учителем, использующих линейное разделение объектов в пространстве признаков с помощью гиперплоскости. Метод применяется для решения задачи бинарной классификации. Основной проблемой метода является выбор оптимальной гиперплоскости, которая позволяет разделить классы с максимальной точностью. Для этого разделяющая гиперплоскость должна быть выбрана таким образом, чтобы расстояние междуближайшими точками, расположенными по разные стороны от нее, было бы максимальным. Данное расстояние называется зазором (margin), а сами точки – опорными векторами (support vectors). Тогда разделяющая гиперплоскость должна быть выбрана таким образом, чтобы максимизировать зазор, что обеспечит более уверенное разделение классов.


В данной статье приведен пример решения этой задачи для линейно разделимой выборки. Также исследуется устойчивость алгоритма: зависимость параметров разделяющей гиперплоскости от дисперсии случайной переменной.

Содержание

Постановка задачи линейной классификации

Рассматривается задача обучения по прецедентам \left \langle X,\ Y,\ y*,\ X^\ell \right \rangle - , где X - пространство объектов, Y - множество ответов, y*:\ X \rightarrow Y - целевая зависимость, значения которой известны только на объектах обучающей выборки X=\(x_i,y_i\)_{i=1}^\ell\ ,\ y_i = y*(x_i). Требуется построить алгоритм a:\ X \rightarrow Y, аппроксимирующий целевую зависимость на всём пространстве X.

Требуется построить задачу классификации на два непересекающихся класса, в которой объекты описываются n-мерными вещественными векторами:\ X\ =\ \mathbb{R}^n,\ Y\ =\ \{-1,+1\}.

Будем строить линейный пороговый классификатор:

a(x)\ =\ sign(\sum_{j=1}^n w_jx^j\ -\ w_0)\ =\ sign(<w,x>\ -\ w_0),

где x\ =\ (x^1,...,x^n) - признаковое описание объекта x; вектор w\ =\ (w^1,...,w^n)\ \in\ \mathbb{R} и скалярный порог w_0\ in\ \mathbb{R} являются параметрами алгоритма.

Уравнение <w,x>\ =\ w_0 описывает гиперплоскость, разделяющую классы в про- странстве \mathbb{R}^n.

Описание алгоритма

Понятие оптимальной разделяющей гиперплоскости

Предположим, что выборка X=\(x_i,y_i\)_{i=1}^\ell\ линейно разделима. Тогда существуют значения параметров w,\ w_0, при которых функционал числа ошибок

Q(w,w_0)\ =\ \sum_{i=1}^\ell [y_i(<w,x_i>\ -\ w_0)\ <\ 0]

принимает нулевое значение. Но тогда разделяющая гиперплоскость не единствен- на. Можно выбрать другие её положения, реализующие такое же разбиение выборки на два класса. Идея метода заключается в том, чтобы разумным образом распоря- диться этой свободой выбора.

Потребуем, чтобы разделяющая гиперплоскость максимально далеко отстояла от ближайших к ней точек обоих клас- сов. Первоначально данный принцип классификации возник из эвристических сооб- ражений: вполне естественно полагать, что максимизация зазора (margin) между классами должна способствовать более надёжной классификации.

Заметим, что параметры линейного порогового классификатора опре- делены с точностью до нормировки: алгоритм a(x) не изменится, если w и w_0 одно- временно умножить на одну и ту же положительную константу. Удобно выбрать эту константу таким образом, чтобы для всех пограничных (т. е. ближайших к разделя- ющей гиперплоскости) объектов x_i из X^\ell выполнялись условия

<w,x_i>\ -\ w_0\ =\ y_i.

Сделать это возможно, поскольку при оптимальном положении разделяющей гипер- плоскости все пограничные объекты находятся от неё на одинаковом расстоянии. Остальные объекты находятся дальше. Таким образом, для всех x_i\ \in\ X^\ell

(1)

<w,x_i> - w_0 \begin{cases} \le -1, & \mbox{if }y_i=-1; \\ \ge 1, & \mbox{if }y_i=+1. \end{cases}

Условие -1\ <\ \left \Big\langle w,x \right \Big\rangle -w_0<\ 1\ задаёт полосу, разделяющую классы. Ширина полосы, как не сложно показать, равна \frac{2}{||w||}. Она максимальна, когда норма вектора w минимальна.

Линейно разделимая выборка

Построение оптимальной разделяющей гиперплоскости сводится к минимизации квадратичной формы при \ell ограничениях-неравенствах вида (1) относительно n+1 переменных w,\ w_0:

\left{<w,w>\rightarrow min\\y_i(<w,x_i>-w_0)\ge1,\qquad i=1,...,\ell\\ \right.

Используя аппарат функций Лагранжа, перейдем к решению двойственной задаче. Несложно показать эквивалентность этой задачи и следующей:

\left{-\mathcal{L}(\lambda)=-\sum\limits_{i=1}^\ell\lambda_i+\frac{1}{2}\sum\limits_{i=1}^\ell\sum\limits_{j=1}^\ell\lambda_i\lambda_jy_iy_j(<x_i,x_j>)\rightarrow \min\limits_\lambda \\ \lambda_i\ge 0\quad, i=1,...,\ell\\ \sum\limits_{i=1}^\ell\lambda_iy_i=0\quad\right.

Вектор весов будем искать в ввиде w = \sum\limits_{i=1}^l\lambda_ix_iy_i. Для определения порога w_0 достаточно взять произвольный опорный вектор x_i и выразить w_0 из равенства w_0=<w,x_i>-y_i. На практике для повышения численной устойчивости лучше взять в качестве w_0 медиану: w_0=med\{<w_i,x_i>-y_i:\ \lambda_i>0,\ i=1,...,\ell\}. Параметры полосы найдены и можно строить разделяюую полосу.

Исследование на устойчивость алгоритма SVM для линейно разделимой выборки

SVM алгоритм используем матрицу \mathbf{x}^T\mathbf{x}. Проверим, устойчив ли SVM алгоритм? Предположим что дана выбрка

\{ \mathbf{x}_0 = \mathbf{0},\mathbf{x}_1 = \sigma \mathbf{e}_1,...,\mathbf{x}_m = \sigma \mathbf{e}_m\} \in \mathbb{R}^m
\{ y_0 = -1,y_1 = 1,...,y_m = 1\}

В этом случае задача SVM сводится к задаче

\left{\frac{1}{2}\sum\limits_{i=1}^m\alpha_i^2\sigma_i^2-2\sum\limits_i\alpha_i \rightarrow \min\limits_\alpha \\\alpha_i\ge 0,i=1,...,m


где \alpha_0=\sum\limits_{i=1}^m\alpha_i .

Приведенная задачи имеет решение \left ( \alpha_0^*, \frac{2}{\sigma_1^2},...,\frac{2}{\sigma_m^2} \right )

где \alpha_0^*=\sum\limits_{i=1}^m\frac{2}{\sigma_i^2},\mathbf{w}=\left ( \frac{2}{\sigma_1^2},...,\frac{2}{\sigma_m^2} \right ), и b=1.

Теперь пусть \sigma_i=2^{-i},\ i=1,...,80. В этом случае решение задается формулами \alpha_0^*=2\sum\limits_{i=1}^{80}{(2^i)}^2 и \alpha_i^*=2{(2^i)}^2,\ i=1,...,80, где \mathbf{w}=2(2^1,...,2^{80}) и b=1

На самом деле, \alpha_0^*=2\sum\limits_{i=1}^m\alpha_i^* накладывает ограничения на точность результатов.

SVM алгоритм \mathbf{x}^T\mathbf{x} численно нестабилен.

Вычислительный эксперимент

Смотри также


Данная статья является непроверенным учебным заданием.
Студент: Участник:Алексей Морозов
Преподаватель: Участник:В.В.Стрижов
Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.recognition.su/wiki/index.php?title=SVM_%D0%B4%D0%BB%D1%8F_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%BE_%D1%80%D0%B0%D0%B7%D0%B4%D0%B5%D0%BB%D0%B8%D0%BC%D0%BE%D0%B9_%D0%B2%D1%8B%D0%B1%D0%BE%D1%80%D0%BA%D0%B8_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты