Робастное оценивание

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 12: Строка 12:
=== Оценки типа максимального правдоподобия (<tex>M-</tex>оценки)===
=== Оценки типа максимального правдоподобия (<tex>M-</tex>оценки)===
 +
Всякая оценка <tex>T_n</tex>
 +
 +
<tex>\sum_{i=1}^n \rho (x_i;T_n) \rightarrow \min</tex>
 +
 +
<tex>\sum_{i=1}^n \psi (x_i;T_n) = 0</tex>
== Вычисление робастных оценок ==
== Вычисление робастных оценок ==

Версия 20:18, 5 января 2010

Содержание

Введение

На протяжении последних десятилетий росло понимание того факта, что некоторые наиболее распространенные статистические процедуры (в том числе те, которые оптимальны в предположении о нормальности распределения) весьма чувствительны к довольно малым отклонениям от предположений. Вот почему теперь появились иные процедуры - "робастные" (от англ. robust - крепкий,здоровый, дюжий).

Мы будем понимать под термином робастность нечувствительность к малым отклонениям от предположений. Процедура робастна, если малые отклонения от предположенной модели должны ухудшать качество процедуры (например, асимптотика дисперсии или уровень значимости и мощность критерия) должны быть близки к номинальным величинам, вычисленным для принятой модели.

Рассмотрим робастность по распределению, т.е. ситуации, в которых истинная функция распределения незначительно отличается от предполагаемой в модели (как правило, гауссовской функции распределения). Это не только наиболее важный случай, но и наиболее полно изученный. Гораздо меньше известно о том, что происходит в тех ситуациях, когда несколько нарушаются прочие стандартные допущения статистики, и том, какие меры защиты должны предусматриваться в подобных случаях.

Основные типы оценок

Введем оценки трех основных типов (M,\;\;L,\;\;R),буквы M,\;\;L,\;\;R отвечают соответственно оценкам типа максимального правдоподобия, линейным комбинациям порядковых статистик и оценкам, получаемых в ранговых критериях.

Особое значение имеют M-оценки, это наиболее гибкие оценки - они допускают прямое обобщение на многопараметрический случай.

Оценки типа максимального правдоподобия (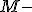M-оценки)

Всякая оценка T_n

\sum_{i=1}^n \rho (x_i;T_n) \rightarrow \min

\sum_{i=1}^n \psi (x_i;T_n) = 0

Вычисление робастных оценок

Рассмотрим пример. Для оценки p неизвестных параметров \theta_1,\; \dots ,\theta_p используется n наблюдений y_1,\; \dots,y_n, причем они связаны между собой следующим неравенством \mathbf{y}=X\mathbf{\theta}+\mathbf{u}, где элементы матрицы X суть известные коэффициенты, а \mathbf{u} - вектор независимых случайных величин,имеющих (приблизительное)одинаковые функции распределения.

Тогда решение сводится к следующему: |\mathbf{y}-X\mathbf{\theta}|^2 \rightarrow \min

Если матрица X - матрица полного ранга p, то \hat \theta={(X^{T}X)}^{-1}X^T\mathbf{y}, а оценки \hat y_i будут высиляться по следующей формуле \hat{\mathbf{y}} = H\mathbf{y}, где H=X{(X^{T}X)}^{-1}X^T, далее H - матрица подгонки.

Допустим, что мы получили значения \hat y_i и остатки r_i=y_i-\hat y_i.

Пусть s_i - некоторая оценка стандартной ошибки наблюдений y_i (или стандартной ошибки остатков r_i)

Метрически винзоризуем наблюдения y_i, заменяя их псевдонаблюдениями {y_i}^{\ast}:

{y_i}^{\ast}= \left{ y_i\,, \; \;\; |r_i| \le cs_i \\ \hat y_i - cs_i\,, \;\; r_i<-cs_i \\ \hat y_i + cs_i\,, \;\; r_i>cs_i \right.

Константа c регулирует степень робастности, её значения хорошо выбирать из промежутка от 1 до 2, например, чаще всего c=1.5.

Затем по псевдонаблюдениям y_i^{\ast} вычисляются новые значения \hat{y_i} подгонки (и новые s_i). Действия повторяются до достижения сходимости.

Если все наблюдения совершенно точны, то классическая оценка дисперсии отдельного наблюдения имеет вид s^2=\frac{1}{n-p}\sum{r_i^2}, и стандартную ошибку остатка r_i можно в этом случае оценивать величиной s_i=\sqrt{1-h_i}s, где h_i есть i-й диагональный элемент матрицы H.

При использовании вместо остатков r_i модифицированных остатков r_i^{\ast}=y_i^{\ast}- \hat y_i , как нетрудно видеть, получается заниженная оценка масштаба. Появившееся смещение можно ликвидировать, полагая (в первом приближении)

s^2=\frac{1}{n-p}\sum{{r_i}^{\ast2}/(\frac{m}{n})^2},

где n-p - число наблюдений без числа параметров, m - число неизменных наблюдений (y_i^{\ast}=y_i).

Очевидно, что эта процедура сводит на нет влияние выделяющихся наблюдений.


Литература

  1. Хьюбер П. Робастность в статистике. — М.: Мир, 1984.

Ссылки

См. также


Данная статья является непроверенным учебным заданием.
Студент: Участник:Джумабекова Айнагуль
Преподаватель: Участник:Vokov
Срок: 6 января 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.


Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A0%D0%BE%D0%B1%D0%B0%D1%81%D1%82%D0%BD%D0%BE%D0%B5_%D0%BE%D1%86%D0%B5%D0%BD%D0%B8%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5»