Материал из MachineLearning.
(Различия между версиями)
|
|
| Строка 1: |
Строка 1: |
| - | * [[Двухфакторная непараметрическая модель]]: [[критерий Фридмана]] [Лапач, 203], [[критерий Пейджа]]. Примеры: сравнение эффективности методов производства, агротехнических приёмов.
| |
| - |
| |
| - | '''Данные.'''
| |
| - |
| |
| - | В каждом из <tex>n</tex> блоков содержится по одному наблюдению <tex>x_{ij}</tex>
| |
| - | на каждуб из <tex>k</tex> обработок. Будем считать наблюдения реализацией случайных велечин
| |
| - | <tex>X_{ij}</tex> в модели
| |
| - |
| |
| - | <tex>X_{ij} = \mu + \alpha_i + \beta_j + \epsilon_{ij}</tex>,
| |
| - | где <tex>1 \le i \le n, 1 \le j \le k, </tex>.
| |
| - |
| |
| - | Здесь <tex>\mu</tex> - неизвестное общее среднее,
| |
| - | <tex>\alpha_i</tex> - эффект блока <tex>i</tex> (неизвестный мешающий параметр),
| |
| - | <tex>\beta_j</tex> - эффект блока <tex>j</tex> (интересующий нас параметр),
| |
| - | <tex>\epsilon_{ij}</tex> - случайная ошибка
| |
| - | <tex>j</tex>
| |
| - |
| |
| - | '''Допущения.'''
| |
| - |
| |
| - | '''1.''' Все ошибки <tex>\epsilon_{ij}</tex> независимы.
| |
| - |
| |
| - | '''2.''' Все <tex>\epsilon_{ij}</tex> имеют одинаковое непрерывное (неизвестное) распределение.
| |
| - |
| |
| - | ==Критерий Фридмана==
| |
| - |
| |
| - | Для проверки гипотезы
| |
| - |
| |
| - | <tex> H_0: \beta_1 = \dots = \beta_k </tex>
| |
| - |
| |
| - | против альтернативы
| |
| - |
| |
| - | <tex> H_1 </tex>: не все <tex> \beta_j </tex> равны между собой
| |
| - |
| |
| - | применяется [[Критерий Фридмана]] [Холлендер М., Вульф Д.А., 155; Лагутин М. Б., 260]
| |
| - |
| |
| - | ===Пример===
| |
| - | Д. Хебб и К.Уильямс разработали тест эстакадного лабиринта для сравнительной оценки "сообразительности" животных. Он состоит из 12 заданий. Есть данные средних чисел ошибок при выполнении этих заданий крысами, кроликами и кошками. Есть ли животные, которые значимо различаются?
| |
| - |
| |
| - | ==Критерий Пейджа==
| |
| - |
| |
| - | Нередко условия эксперимента таковы, что обработки упорядочены естественным образом, например, по интенсивности стимулов, сложности заданий и т.п. Критерий Пейджа учитывает информацию, содержащуюся в предпологаемой ''упорядоченности'' (в отличие от критерия Фридмана, статистика которого принимает одно и то же значение для всех перенумераций обработок).
| |
| - |
| |
| - | Для проверки гипотезы
| |
| - |
| |
| - | <tex> H_0: \beta_1 = \dots = \beta_k </tex>
| |
| - |
| |
| - | против альтернативы возрастания эффектов обработок
| |
| - |
| |
| - | <tex> H_2: \beta_1 \leq \dots \leq \beta_k </tex>,
| |
| - |
| |
| - | где хотя бы одно из неравенств строгое,
| |
| - |
| |
| - | выполняется [[Критерий Пейджа|статистика критерия Пейджа]] [Холлендер М., Вульф Д.А., 163; Лагутин М. Б., 263]
| |
| - |
| |
| - | ===Пример===
| |
| - | '''Прочность волокон хлопка.'''
| |
| - |
| |
| - | Проведен опыт, в котором изучалось влияние колличества калорий удобрения, вносимого в почву, на разрывную прочность волокон хлопка. С каждой делянки отбирался один образец хлопка, на котором 4 измерительных показателя прочности по Прессли. Даны данные по этим четырем замерам.
| |
| - | С помощью критерия Пейджа проверить гипотезу об отсутствии влияния количества удобрения на прочность нити, против альтернативы убывания прочности с ростом количества удобрения.
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - |
| |
| - | ==Литература==
| |
| - |
| |
| - | # ''Шеффе Г.'' Дисперсионный анализ. — М., 1980.
| |
| - | # ''Аренс Х.'' ''Лёйтер Ю.'' Многомерный дисперсионный анализ.
| |
| - | # ''Лапач С. Н. , Чубенко А. В., Бабич П. Н.'' Статистика в науке и бизнесе. — Киев: Морион, 2002.
| |
| - | # ''Лагутин М. Б.'' Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.
| |
| - | # ''Холлендер М., Вульф Д.А.'' Непараметрические методы статистики.
| |
| - |
| |
| - | == Ссылки ==
| |
| - |
| |
| - | * [http://www.tspu.tula.ru/res/math/mop/lections/lection_7.htm#_Toc73845987 Дисперсионный анализ для связанных выборок] - Аналитическая статистика.
| |
| - | * [http://lib.socio.msu.ru/l/library?e=d-000-00---001ucheb--00-0-0-0prompt-10---4------0-1l--1-ru-50---20-about---00031-001-1-0windowsZz-1251-00&a=d&cl=CL1&d=HASHe10c3b36c7d751dd18704b.11 Многофакторный дисперсионный анализ] - Электронная библиотека.
| |
| - |
| |
| - | ==См. также==
| |
| - |
| |
| - | * [[Однофакторная параметрическая модель]]
| |
| - | * [[Однофакторная непараметрическая модель]]
| |
| - | * [[Дисперсионный анализ]]
| |
| - |
| |
| - | [[Категория:Прикладная статистика]]
| |
| - | [[Категория:Дисперсионный анализ]]* [[Двухфакторная непараметрическая модель]]: [[критерий Фридмана]] [Лапач, 203], [[критерий Пейджа]]. Примеры: сравнение эффективности методов производства, агротехнических приёмов.
| |
| - |
| |
| | '''Данные.''' | | '''Данные.''' |
| | | | |
Версия 11:12, 16 декабря 2009
Данные.
В каждом из 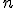 блоков содержится по одному наблюдению
блоков содержится по одному наблюдению 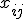 на каждуб из
на каждуб из 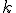 обработок. Будем считать наблюдения реализацией случайных велечин
обработок. Будем считать наблюдения реализацией случайных велечин
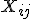 в модели
в модели
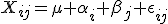 ,
где
,
где 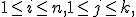 .
.
Здесь 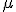 - неизвестное общее среднее,
- неизвестное общее среднее,
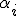 - эффект блока
- эффект блока 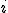 (неизвестный мешающий параметр),
(неизвестный мешающий параметр),
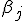 - эффект блока
- эффект блока 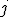 (интересующий нас параметр),
(интересующий нас параметр),
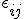 - случайная ошибка
- случайная ошибка
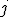
Допущения.
1. Все ошибки 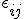 независимы.
независимы.
2. Все 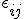 имеют одинаковое непрерывное (неизвестное) распределение.
имеют одинаковое непрерывное (неизвестное) распределение.
Критерий Фридмана
Для проверки гипотезы
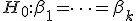
против альтернативы
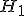 : не все
: не все 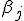 равны между собой
равны между собой
применяется Критерий Фридмана [Холлендер М., Вульф Д.А., 155; Лагутин М. Б., 260]
Пример
Д. Хебб и К.Уильямс разработали тест эстакадного лабиринта для сравнительной оценки "сообразительности" животных. Он состоит из 12 заданий. Есть данные средних чисел ошибок при выполнении этих заданий крысами, кроликами и кошками. Есть ли животные, которые значимо различаются?
Критерий Пейджа
Нередко условия эксперимента таковы, что обработки упорядочены естественным образом, например, по интенсивности стимулов, сложности заданий и т.п. Критерий Пейджа учитывает информацию, содержащуюся в предпологаемой упорядоченности (в отличие от критерия Фридмана, статистика которого принимает одно и то же значение для всех перенумераций обработок).
Для проверки гипотезы
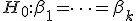
против альтернативы возрастания эффектов обработок
 ,
,
где хотя бы одно из неравенств строгое,
выполняется статистика критерия Пейджа [Холлендер М., Вульф Д.А., 163; Лагутин М. Б., 263]
Пример
Прочность волокон хлопка.
Проведен опыт, в котором изучалось влияние колличества калорий удобрения, вносимого в почву, на разрывную прочность волокон хлопка. С каждой делянки отбирался один образец хлопка, на котором 4 измерительных показателя прочности по Прессли. Даны данные по этим четырем замерам.
С помощью критерия Пейджа проверить гипотезу об отсутствии влияния количества удобрения на прочность нити, против альтернативы убывания прочности с ростом количества удобрения.
Литература
- Шеффе Г. Дисперсионный анализ. — М., 1980.
- Аренс Х. Лёйтер Ю. Многомерный дисперсионный анализ.
- Лапач С. Н. , Чубенко А. В., Бабич П. Н. Статистика в науке и бизнесе. — Киев: Морион, 2002.
- Лагутин М. Б. Наглядная математическая статистика. В двух томах. — М.: П-центр, 2003.
- Холлендер М., Вульф Д.А. Непараметрические методы статистики.
Ссылки
См. также

| Данная статья является непроверенным учебным заданием.
- Студент: Участник:Пасконова Ольга
- Преподаватель: Участник:Vokov
- Срок: 31 декабря 2009
До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru.
По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.
|
блоков содержится по одному наблюдению
на каждуб из
обработок. Будем считать наблюдения реализацией случайных велечин
в модели
,
где
.
- неизвестное общее среднее,
- эффект блока
(неизвестный мешающий параметр),
- эффект блока
(интересующий нас параметр),
- случайная ошибка
независимы.
имеют одинаковое непрерывное (неизвестное) распределение.
: не все
равны между собой
,

