Распределение Фишера

(Различия между версиями)

Версия 15:05, 19 ноября 2009

**Распределение Фишера**
Плотность вероятности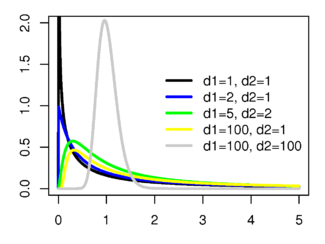
Функция распределения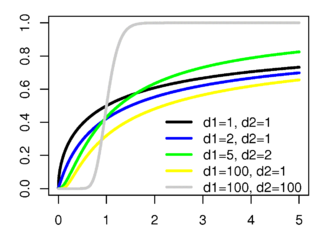
Параметры	$d_1>0,\ d_2>0$ - числа степеней свободы
Носитель	$x \in [0; +\infty)\!$
Плотность вероятности	$\frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}} {(d_1\,x+d_2)^{d_1+d_2}}}} {x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!$
Функция распределения	$I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!$
Математическое ожидание	$\frac{d_2}{d_2-2}\!$ , если $d_2 > 2$
Медиана
Мода	$\frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2}\!$ , если $d_1 > 2$
Дисперсия	$\frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!$ , если $d_2 > 4$
Коэффициент асимметрии	$\frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}\!$ , если $d_2 > 6$
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов	'
Характеристическая функция

Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.

Пусть $Y_1,Y_2$ — две независимые случайные величины, имеющие распределение хи-квадрат: $Y_i \sim \chi^2(d_i)$ , где $d_i \in \mathbb{N},\; i=1,2$ . Тогда распределение случайной величины

$F = \frac{Y_1/d_1}{Y_2/d_2}$ ,

называется распределением Фишера со степенями свободы $d_1$ и $d_2$ . Пишут $F \sim \mathrm{F}(d_1,d_2)$ .

Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:

$\mathbb{M}[F] = \frac{d_2}{d_2 - 2}$ , если $d_2 > 2$ ,

$\mathrm{D}[F] = \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!$ , если $d_2 > 4$ .

$\frac{1}{F} \sim \mathrm{F}(d_2, d_1)$ .

Распределение Фишера сходится к единице: если $F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2)$ , то

$F_{d_1,d_2} \to \delta(x-1)$ по распределению при $d_1,d_2 \to \infty$ ,

где $\delta(x-1)$ — дельта-функция в единице, то есть распределение случайной величины-константы $X \equiv 1$ .

Если $F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2)$ , то случайные величины $d_1 F_{d_1,d_2}$ сходятся по распределению к $\chi^2(d_1)$ при $d_2 \to \infty$ .

Версия 14:18, 19 ноября 2009 (править) Bogdan (Обсуждение \| вклад) (Новая: {{Вероятностное распределение \| name =Распределение Фишера\| type =Плотность\| pdf_image =[[Изображение:...) ← К предыдущему изменению		Версия 15:05, 19 ноября 2009 (править) (отменить) Pavel Vilenkin (Обсуждение \| вклад) (категория) К следующему изменению →
Строка 46:		Строка 46:

	* Если <tex>F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2)</tex>, то случайные величины <tex>d_1 F_{d_1,d_2}</tex> сходятся по распределению к <tex>\chi^2(d_1)</tex> при <tex>d_2 \to \infty</tex>.		* Если <tex>F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2)</tex>, то случайные величины <tex>d_1 F_{d_1,d_2}</tex> сходятся по распределению к <tex>\chi^2(d_1)</tex> при <tex>d_2 \to \infty</tex>.
		+
		+	[[Категория:Вероятностные распределения]]