Коэффициент корреляции Пирсона

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→См. также)
(→Определение)
Строка 7: Строка 7:
<tex>x=\left( x_1, \cdots ,x_n \right), \; y=\left( y_1, \cdots ,y_n \right) </tex>;
<tex>x=\left( x_1, \cdots ,x_n \right), \; y=\left( y_1, \cdots ,y_n \right) </tex>;
-
Коэффициент корреляции Пирсена рассчитывается по формуле:
+
Коэффициент корреляции Пирсона рассчитывается по формуле:
<tex>r_{xy} = \frac {\sum_{i=1}^{n} \left( x_i-\bar{x} \right)\left( y_i-\bar{y} \right)}{\sqrt{\sum_{i=1}^{n} \left( x_i-\bar{x} \right)^2 \sum_{i=1}^{n} \left( y_i-\bar{y} \right)^2}} = \frac {cov(x,y)}{\sqrt{S_x^2S_y^2}} </tex>
<tex>r_{xy} = \frac {\sum_{i=1}^{n} \left( x_i-\bar{x} \right)\left( y_i-\bar{y} \right)}{\sqrt{\sum_{i=1}^{n} \left( x_i-\bar{x} \right)^2 \sum_{i=1}^{n} \left( y_i-\bar{y} \right)^2}} = \frac {cov(x,y)}{\sqrt{S_x^2S_y^2}} </tex>

Версия 15:34, 10 января 2009

Содержание

Определение

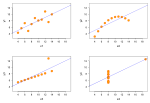
Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя величинами.

Даны две выборки

x=\left( x_1, \cdots ,x_n \right), \; y=\left( y_1, \cdots ,y_n \right) ;

Коэффициент корреляции Пирсона рассчитывается по формуле:

r_{xy} = \frac {\sum_{i=1}^{n} \left( x_i-\bar{x} \right)\left( y_i-\bar{y} \right)}{\sqrt{\sum_{i=1}^{n} \left( x_i-\bar{x} \right)^2 \sum_{i=1}^{n} \left( y_i-\bar{y} \right)^2}} = \frac {cov(x,y)}{\sqrt{S_x^2S_y^2}}

где

\bar{x}, \; \bar{y} - средние значения выборок x и y;

S_x, \; S_y - среднеквадратичные отклонения;

r_{xy} \in \left[-1,1\right] − называют также теснотой линейной связи.

  • \left| r_{xy} \right| =1 , тогда x, y - линейно зависимы.
  • r_{xy}=0, тогда x, y - линейно независимы.

Статистическая проверка наличия корреляции

Гипотеза H_0: Отсутствие линейной связи r_{xy} = 0

Статистика критерия:

T = \frac{2xy\sqrt{n-2}}{sqrt{1-2x^2y^2}} \sim t_{n-2} - Распределение Стьюдента с n-2 степенями свободы.

Слабые стороны

  • Четыре различных набора данных, коэффициент корреляции на которых равен 0.81
    Четыре различных набора данных, коэффициент корреляции на которых равен 0.81
    Неустойчивость к выбросам;
  • С помощью коэффициента корреляции можно определить линейную зависимость между величинами, другие взаимосвязи выявляются методами регрессионного анализа;
  • Необходимо понимать различие понятий "независимость" и "некоррелированность". Из первого следует второе, но не наоборот.

Для того, чтобы выяснить отношение между двумя переменными, часто необходимо избавиться от влияния третьей переменной. Рассмотрим пример 3-х переменных: x,y,z. Исключим влияние переменной z:

r_{xy \setminus z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{ \left(\ 1-r_{xz} \right)^2 \left(\ 1-r_{yz} \right)^2}}

Для исключения влияния большего числа переменных:

r_{ij \setminus vars}=\frac{-R_{ij}}{\sqrt{R_{ii}R_{jj}}}

R_{ij} = (-1)^{i+j}M_{ij} , где M_{ij} - гл. минор матрицы коэффициентов корреляции переменных R = \begin{pmatrix} 1 & r_{12} & \dots & r_{1k} \\ r_{21} & 1 & \dots & r_{2k}\\ \vdots & & & \vdots \\ r_{k1} & \dots & \dots & 1 \end{pmatrix} ;

Литература

См. также

Ссылки

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D1%8F%D1%86%D0%B8%D0%B8_%D0%9F%D0%B8%D1%80%D1%81%D0%BE%D0%BD%D0%B0»
Личные инструменты