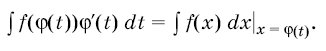Участник:Пасконова Ольга/Песочница
Материал из MachineLearning.
(Различия между версиями)
(→Формула замены переменных в неопределенном интеграле) |
(→Формула замены переменных в неопределенном интеграле) |
||
| Строка 7: | Строка 7: | ||
Пусть функции <tex> f(x)</tex> и <tex> \phi(x) </tex> определены соответственно на промежутках <tex> \Delta_x </tex> и <tex> \Delta_y </tex>, причем <tex> \phi(\Delta_t) \subset \Delta_x </tex>. Если функция <tex> f </tex> имеет на <tex> \Delta_x </tex> первообразную <tex> F{x)</tex> и, следовательно, | Пусть функции <tex> f(x)</tex> и <tex> \phi(x) </tex> определены соответственно на промежутках <tex> \Delta_x </tex> и <tex> \Delta_y </tex>, причем <tex> \phi(\Delta_t) \subset \Delta_x </tex>. Если функция <tex> f </tex> имеет на <tex> \Delta_x </tex> первообразную <tex> F{x)</tex> и, следовательно, | ||
| - | + | [[Изображение:Q1.png]] | |
а функция <tex> \phi(x) </tex> дифференцируема на <tex> \Delta_t </tex>, то функция | а функция <tex> \phi(x) </tex> дифференцируема на <tex> \Delta_t </tex>, то функция | ||
| - | <tex> f(\phi(t))\phi^`(t) </tex> имеет на <tex> \Delta_t </tex>, первообразную <tex> F(\phi(t)) </tex> и | + | <tex> f(\phi(t))\phi^`(t) </tex> имеет на <tex> \Delta_t </tex>, первообразную <tex> F(\phi(t)) </tex> и [[Изображение:Q2.png]] |
Версия 12:27, 16 ноября 2008
Формула замены переменных в неопределенном интеграле
Рассмотрим свойство неопределенного интеграла, часто оказывающееся полезным при вычислении первообразных элементарных функций.
Теорема.
Пусть функции и
определены соответственно на промежутках
и
, причем
. Если функция
имеет на
первообразную
и, следовательно,
![]() а функция
а функция дифференцируема на
, то функция
имеет на
, первообразную
и