Вычисление определителя
Материал из MachineLearning.
(→Постановка задачи) |
(→Алгоритм решения) |
||
| Строка 7: | Строка 7: | ||
== Алгоритм решения == | == Алгоритм решения == | ||
| - | |||
| - | |||
| - | |||
=== Определитель === | === Определитель === | ||
Версия 15:50, 20 октября 2008
| | Название статьи необходимо изменить. Текст статьи нуждается в существенной переработке (см. Обсуждение).--Strijov 12:53, 20 октября 2008 (MSD) |
Содержание |
Постановка задачи
Задание подразумевает знакомство пользователя с основными понятиями численных методов, такими как определитель и обратная матрица, и различными способами их вычислений. В данном теоретическом отчете простым и доступным языком сначала вводятся основные понятия и определения, на основании которых проводится дальнейшее исследование. Данная работа подразумевает, что пользователь может не иметь специальных знаний в области численных методов и линейной алгебры, но с легкостью сможет воспользоваться результатами работы. Для наглядности приведена программа вычисления определителя матрицы несколькими методами, написанная на языке программирования C++. Программа используется как лабораторный стенд для создания иллюстраций к отчету. А также проводится исследование методов для решения систем линейных алгебраических уравнений. Доказывается бесполезность вычисления обратной матрицы, поэтому в работе приводится более оптимальные способы решения уравнений не вычисляя ее. Рассказывается почему существует такое количество различных методов вычисления определителей и обратных матриц и разбираются их недостатки. Также рассматриваются погрешности при вычислении определителя и оценивается достигнутая точность. Помимо русских терминов в работе используются и их английские эквиваленты для понимания, под какими названиями искать численные процедуры в библиотеках и что означают их параметры.
Алгоритм решения
Определитель
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка
. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы будем обозначать
или det
.
Определение 1. Определителем квадратной матрицы 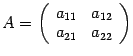 второго порядка называется число
второго порядка называется число ![]() .
.
Определителем 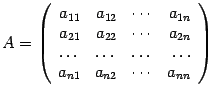 квадратной матрицы порядка
квадратной матрицы порядка ,
, называется число
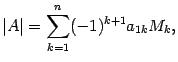
где - определитель матрицы порядка
, полученной из матрицы
вычеркиванием первой строки и столбца с номером
.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка: 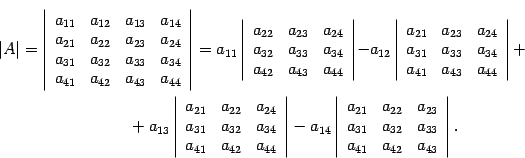
Замечание. Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание. В определении 1 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел.
Замечание. В литературе вместо термина "определитель" используется также термин "детерминант", имеющий тот же самый смысл. От слова "детерминант" и появилось обозначение det .
Рассмотрим некоторые свойства определителей, которые сформулируем в виде утверждений.
Обратная матрица
Вычисление определителя и обратной матрицы с помощью метода Гаусса
Прагматика
Классификация методов
Обращение матрицы методом Гаусса
Вычисление определителя методом триангуляции
Примеры работы алгоритма
Руководство пользователя
Руководство программиста
Литература
- http://e-lib.gasu.ru/eposobia/metody/
- http://www.exponenta.ru/educat/systemat/slivina/lection/lection2/lection2.asp
- http://elib.ispu.ru/library/math/sem1/index.html
- Киселёв В.Ю., Пяртли А.С., Калугина Т.Ф. Высшая математика.
- Боглаев Ю.П. Вычислительная математика и программирование. - М., Высшая школа, 1990, 544с.

