Биномиальное распределение

Материал из MachineLearning.

(Различия между версиями)

Версия 13:01, 20 декабря 2012

**Биномиальное распределение**
Функция вероятности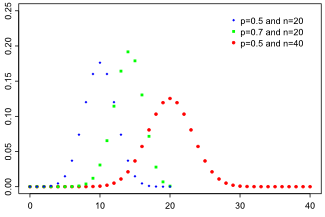
Функция распределения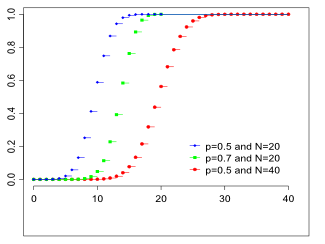
Параметры	$n \geq 0$ — число «испытаний» $0\leq p \leq 1$ — вероятность «успеха»
Носитель	$k \in \{0,\ldots,n\}\!$
Функция вероятности	${n \choose k}\,p^k q^{n-k} \!$
Функция распределения	$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Математическое ожидание	$np\!$
Медиана	одно из $\{[np]-1, [np], [np]+1\}$
Мода	$\lfloor (n+1)\,p\rfloor\!$
Дисперсия	$npq\!$
Коэффициент асимметрии	$\frac{1-2p}{\sqrt{npq}}\!$
Коэффициент эксцесса	$\frac{1-6pq}{npq}\!$
Информационная энтропия	$\frac12 \log_2 \big( 2\pi e\, np(1-p) \big) + O \left( \frac{1}{n} \right)$
Производящая функция моментов	$(q + pe^t)^n \!$
Характеристическая функция	$(q + pe^{it})^n \!$

Содержание

1 Определение
2 Основные свойства
3 Асимптотические приближения при больших
4 Литература
5 Ссылки
6 Интерпретация 21-го века
7 Биномиальная схема повторных циклов случайных зависимых экспериментов
8 Биномиальное распределение — совместное распределение двух случайных величин ^[1]
9 Характер зависимости случайных величин в каждом цикле экспериментов:
10 Характеристики случайных величин биномиального распределения:
11 Характеристики биномиального распределения:
12 Математическое ожидание биномиального распределения
13 Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами
14 Сравнительная оценка характеристик биномиальных распределений настоящей и традиционной интерпретаций
15 Связь с другими распределениями

Определение

Биномиальное распределение — дискретное распределение вероятностей случайной величины $X,$ принимающей целочисленные значения $k=0,1,\ldots,n$ с вероятностями:

$P(X=k)={n \choose k}p^k(1-p)^{n-k}.$

Данное распределение характеризуется двумя параметрами: целым числом $n>0,$ называемым числом испытаний, и вещественным числом $p,$ $0\le p\le 1,$ называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из $n$ независимых испытаний, в каждом из которых может произойти "успех" с вероятностью $p,$ то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы $X=X_1+\cdots+X_n$ независимых слагаемых, имеющих распределение Бернулли.

Основные свойства

Характеристическая функция: $\phi(t)=(1+p(e^{it}-1))^n.$

Моменты:

Математическое ожидание: $MX=np.$
Дисперсия: $DX=np(1-p).$
Асимметрия: $\gamma_1=\frac{1-2p}{\sqrt{np(1-p)}};$ при $p=0.5$ распределение симметрично относительно центра $n/2.$

Асимптотические приближения при больших 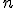$n$

Если значения $n$ велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).

Приближение Пуассона

Приближение распределением Пуассона применяется в ситуациях, когда значения $n$ большие, а значения $p$ близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром $\lambda=np.$

Строгая формулировка: если $n\to\infty$ и $p\to 0$ таким образом, что $np\to\lambda,$ то

$P(X=k)\to\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0, 1, 2, \ldots$

Более того, справедлива следующая оценка. Пусть $Y$ — случайная величина, имеющая распределение Пуассона с параметром $\lambda=np.$ Тогда для произвольного множества $B\subset\{0,1,2,\ldots\}$ справедливо неравенство:

$|P(X\in B) - P(Y\in B)|\le 2np^2.$

Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12].

Нормальное приближение

Приближение нормальным распределением используется в ситуациях, когда $n\to\infty,$ а $p$ фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении $X$ в виде суммы $n$ слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины

$X'=\frac{X-MX}{\sqrt{DX}}=\frac{X-np}{\sqrt{npq},$ где $q=1-p,$

близко к стандартному нормальному.

Локальная теорема Муавра-Лапласа

Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям $k,$ таким что $|k-np|=o(npq)^{2/3},$ имеет место

$P(X=k)\sim\frac{1}{\sqrt{2\pi npq}}e^{-\frac{(k-np)^2}{2npq}}=\frac{1}{\sqrt{npq}}\varphi\left(\frac{k-np}{\sqrt{npq}}\right),$

где $\varphi$ — плотность стандартного нормального распределения.

Интегральная теорема Муавра-Лапласа

На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает нечасто. Гораздо более важно оценивать вероятности событий, включающих в себя множество значений. Для этого используется интегральная теорема, которую можно сформулировать в следующем виде [1, гл. I, §6]:

$\sup_{-\infty\le a<b\le\infty}\left|P\left(a<\frac{X-np}{\sqrt{npq}}\le b\right) - P(a<Z\le b)\right|\to 0$ при $n\to\infty,$

где случайная величина $Y$ имеет стандартное нормальное распределение $\mathcal{N}(0,1),$ и аппроксимирующая вероятность определяется по формуле

$P(a<Z\le b)=\Phi(b)-\Phi(a),$

где $\Phi(t)$ — функция распределения стандартного нормального закона: $\Phi(t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^t e^{-t^2/2}\,dt.$

Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена:

$\sup_{-\infty\le x\le\infty}|F_n(x)-\Phi(x)|\le\frac{p^2+q^2}{\sqrt{npq}},$

где $F_n(x)$ — функция распределения случайной величины $X'=\frac{X-np}{\sqrt{npq}}.$ На практике решение о том, насколько следует доверять нормальному приближению, принимают исходя из величины $npq.$ Чем она больше, тем меньше будет погрешность приближения.

Заметим, что асимптотический результат не изменится, если заменить строгие неравенства на нестрогие и наоборот. Предельная вероятность от такой замены также не поменяется, так как нормальное распределение абсолютно непрерывно и вероятность принять любое конкретное значение для него равна нулю. Однако исходная вероятность от такой замены может измениться, что вносит в формулу некоторую неоднозначность. Для больших значений $n$ изменение будет невелико, однако для небольших $n$ это может внести дополнительную погрешность.

Для устранения этой неоднозначности, а также повышения точности приближения рекомендуется задавать интересующие события в виде интервалов с полуцелыми границами. При этом приближение получается точнее. Это связано с тем интуитивно понятным соображением, что аппроксимация кусочно-постоянной функции (функции распределения биномиального закона) с помощью непрерывной функции дает более точные приближения между точками разрыва, чем в этих точках.

Пример

Пусть $n=20,$ $p=0.5.$ Оценим вероятность того, что число успехов будет отличаться от наиболее вероятного значения $10$ не более чем на $3$ . Заметим, что значение $npq=5$ очень мало, поэтому применение нормального приближения здесь довольно ненадежно.

Точная вероятность рассматриваемого события равна

$P(7\le X\le 13)\approx 0.8846.$

Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое):

$P(7\le X\le 13)=P(6<X\le 13)=P\left(\frac{6-10}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{13-10}{\sqrt{5}}\right)=P\left(-\frac{4}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{3}{\sqrt{5}}\right)\approx P\left(-\frac{4}{\sqrt{5}}<Z\le\frac{3}{\sqrt{5}}\right)=\Phi\left(\frac{3}{\sqrt{5}}\right) - \Phi\left(-\frac{4}{\sqrt{5}}\right)\approx 0.8733.$

Ошибка приближения равна $0.0113$ .

Теперь построим приближение, используя интервал с концами в полуцелых точках:

$P(7\le X\le 13)=P(6.5<X< 13.5)=P\left(-\frac{3.5}{\sqrt{5}}<\frac{X-np}{\sqrt{npq}}\le\frac{3.5}{\sqrt{5}}\right)\approx P\left(-\frac{3.5}{\sqrt{5}}<Z\le\frac{3.5}{\sqrt{5}}\right)=\Phi\left(\frac{3.5}{\sqrt{5}}\right) - \Phi\left(-\frac{3.5}{\sqrt{5}}\right)\approx 0.8824.$

Ошибка приближения равна $0.0022$ — примерно в 5 раз меньше, чем в предыдущем подходе.

Литература

1. Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.

Ссылки

Биномиальное распределение (Википедия)
Binomial distribution (Wikipedia)

Интерпретация 21-го века

Таблица 1 – Характеристики биномиального распределения интерпретации 21-го века
Пространство элементарных событий	$\sum_{i=1}^2\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})$
Вероятность	$\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1}p_2^{n_2}$
Максимальная вероятность (при математическом ожидании распределения)	$\left(\frac{n!}{n_i!n_2!}p_1^{n_1}p_2^{n_2}\right)_{max}= \frac{1}{2}$
Математическое ожидание (как максимальное произведение математических ожиданий случайных величин)	$\left(\prod_{i=1}^2E(t_i, X_i=n_i \mid t_{i-1},X_{i-1})\right)_{max}=\frac{1}{2}$
Дисперсия	$\sum_{i=1}^2D(t_i,X_i \mid t_{i-1},X_{i-1})=\sum_{i=1}^2(n-n_{i-1})p_iq_i$
Максимальная дисперсия (при математическом ожидании распределения)	$D(X_1,X_2\|X_1)_{max}=\left(\sum_{i-1}^2(n-n_{i-1})p_iq_i \right)_{max}=\frac{3}{4}$
Ковариационная матрица	$B=\\| b_{ij} \\|$ , где : $\rho _{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j\end{cases}$
Корреляционная матрица	$P=\\| \rho_{ij} \\|$ , где $\rho_{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j\end{cases}$
$\chi^2$ - критерий	$\chi^2=\sum_{i=1}^2 [X_i-(n -n_{i-1})p_i^{(0)}]^2/(n -n_{i-1})p_i^{(0)}=$ $=-n+\sum_{i=1}^2X_i^2 /(n-n_{i-1})p_i^{(0)}$

Биномиальная схема повторных циклов случайных зависимых экспериментов

Каждый цикл экспериментов осуществляют методом выбора без возвращения в дискретной временной последовательности

$t_1, t_2.$

Каждая из случайных величин распределения

$X_i=n_i \mid X_{i-1}=n_{i-1}$

это $n_i$ наступлений одного события

$x_i, i =1,2$

в $i$ - ый момент времени при условии, что в $(i-1)$ - ый момент произошло $n_{i-1}$ наступлений предшествующего события $x_{i-1}$ , — распределения Бернулли с успехом, вероятности которых $p_i$ нормированы

$p_1+p_2=1$

и неизменны во время проведения экспериментов.

Если в каждом цикле экспериментов вероятность наступления события $x_i$ равна $p_i$ , то биномиальная вероятность равна вероятности того, что при $n$ экспериментах события $x_1, x_2$ наступят $n_1, n_2$ раз соответственно.

Случайная величина биномиального распределения в соответствующей точке дискретной временной последовательности $t_1, t_2$ имеет:

пространство элементарных событий

$\Omega_i(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})= [0\le n_i \le n-n_{i-1}],$

вероятность

$P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})={n-n_{i-1}\choose n_i}p_i^{n_i},$

математическое ожидание

$E(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=( n-n_{i-1})p_i$

и дисперсию

$D(t_i,X_i \mid t_{i-},X_{i-1})=( n -n_{i-1})p_iq_i, \quad q_i=1-p_i .$

Пространство элементарных событий биномиального распределения есть сумма точечных пространств элементарных событий его случайных величин, образующих дискретную последовательность точек $t_1, t_2$ цикла, а вероятность биномиального распределения — произведение вероятностей его случайных величин.

Биномиальное распределение — совместное распределение двух случайных величин ^[1]

$\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1} p_2^{n_2},\qquad \frac{n!}{n_1!n_2!}={n\choose n_1,n_2}= {n \choose n_1}={n\choose n_2},$

$2\le k \le n <\infty, \qquad n_1+n _2=n, \qquad p_1+p_2=1,$

определённых на точечных пространствах элементарных событий

$\Omega_1, \Omega _2$

и принимающих в дискретные последовательные моменты времени

$t_1, t_2, \quad t_i<t_{i+1}$

целые неотрицательные значения

$n_1, n_2,$

взаимосвязанные условием

$n_1 +n_2=n,$

согласно которому

$X_2=n_2 \mid X_1=n_1$

если в первый момент времени $t_1$ первая случайная величина $X_1$ приняла значение

$n_1, \quad 0\le n_1\le n,$

то во второй момент времени $t_2$ вторая случайная величина $X _2$ принимает значение

$n _2, \quad 0\le n_2\le n- n_1.$

Характер зависимости случайных величин в каждом цикле экспериментов:

только первая случайная величина является независимой, а вторая случайная величина зависима от первой;

если первая случайная величина в первый момент времени приняла своё максимально возможное значение, равное $X_1=n$ , то вторая случайная величина во второй момент времени обязана принять своё минимальное (нулевое) значение $X_2=n_2=0$ в противном случае не будет выполнено условие суммирования числовых значений случайных величин распределения, согласно которому $n_1+n _2=n$ ;

если первая случайная величина в первый момент времени приняла своё минимальное (нулевое) значение $X_1=n_1=0$ , то вторая случайная величина во второй момент времени обязана принять своё максимальное значение $X_2=n_2=n$ в противном случае не будет выполнено условие $n_1+n _2=n$ .

Характеристики случайных величин биномиального распределения:

пространство элементарных событий

$\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=[0 \le n_i \le n-n_{i-1}],$

вероятность

$P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})={n-n_{i-1}\choose n_i}p_i^{n_i},$

математическое ожидание

$E(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=(n-n_{i-1})p_i,$

Дисперсия

$D(t_i,X_i \mid t_{i-1},X_{i-1})=(n -n_{i-1})p_iq_i, \quad q_i=1-p_i,$

производящая

$A(s_i)=(1+p_is_i)^{n-n_{i-1}}$

и характеристическая

$f(t_i)=(1+p_ie^{jt_i})^{n-n_{i-1}}$

функции.

Характеристики биномиального распределения:

пространство элементарных событий

$\sum_{i=1}^2\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1}),$

расположенное в точках $t_1, t_2$ временной последовательности,

вероятность

$\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1!n_2!}p_1^{n_1}p_2^{n_2},$

дисперсия

$\sum_{i=1}^2D(t_i,X_i \mid t_{i-1},X_{i-1})=\sum_{i=1}^2(n-n_{i-1})p_iq_i,$

ковариационная матрица $B=\| b_{ij} \|$ , где

$b_{ij} = \begin{cases} (n-n_{i-1})p_iq_i, & i=j,\\0, & i \not= j,\end{cases}$

корреляционная матрица $P=\| \rho_{ij} \|$ , где

$\rho _{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j,\end{cases}$

$\chi^2$ - квадрат критерий для полиномиально распределенных случайных величин

$\chi^2=\sum_{i=1}^2 [X_i-(n -n_{i-1})p_i^{(0)}]^2/(n -n_{i-1})p_i^{(0)}=$

$=-n+\sum_{i=1}^2X_i^2 /(n-n_{i-1})p_i^{(0)}.$

Урновая модель биномиального распределения содержит одну исходную урну и две приёмные урны. В начальный момент времени исходная урна содержит $n$ - множество различимых неупорядоченных элементов, а приёмные урны пусты. Объем каждой из них не менее объёма исходной урны. Нумерация приёмных урн соответствует нумерации случайных величин биномиального распределения.

Первая выборка

$n_1,\quad 0\le n_1\le n$

в первый момент времени направляется в первую приёмную урну с вероятностью $p_1$ каждого элемента.

Во второй момент времени все оставшиеся $n-n_1$ элементы исходной урны, образующие вторую выборку

$n_2,\quad 0\le n-n_1\le n,$

направляются во вторую приёмную урну с вероятностью $p_2$ каждого элемента.

В результате исходная урна пуста, а все её элементы размещены в приёмных урнах.

После обработки результатов разбиения множества на подмножества элементы возвращают на прежнее место, и урновая модель готова к проведению очередного цикла зависимых экспериментов.

Произведение вероятностей попадания $n_1, n_2$ элементов в две приёмные урны есть биномиальное распределение.

Математическое ожидание биномиального распределения

получают одним из двух способов: как максимум произведения математических ожиданий его случайных величин, или как максимум вероятности распределения.

Необходимые

$k=n, \qquad n_i=1, \qquad 0<p_i<1,$

и достаточные

$p_1=p_2=2^{-1}$

условия получения математического ожидания биномиального распределения.

Математическое ожидание

$\left(\prod_{i=1}^2E(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})\right)_{max}=\left(\prod_{i=1}^2(n-n_{i-1})p_i\right)_{max}=\frac{n!}{n^n}=\frac{1}{2},$

максимальная вероятность

$\left(\prod_{i=1}^2P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})\right)_{max}=\left(\frac{n!}{n_i!n_2!}p_1^{n_1}p_2^{n_2}\right)_{max}=\frac{n!}{n^n}= \frac{1}{2}$

равна математическому ожиданию,

максимальная дисперсия

$D(X_1,X_2|X_1)_{max}=\left(\sum_{i-1}^2(n-n_{i-1})p_iq_i \right)_{max}=\frac{n^2-1}{2n}=\frac{3}{4}.$

Пространство элементарных событий биномиального распределения при получении его математического ожидания

$\Omega(t_1, X_1=n_1=1 \mid t_2,X_2=n_2=1)$

расположено в точках $t_1, t_2$ временной последовательности.

Урновая модель получения математического ожидания биномиального распределения содержит одну исходную урну и две приёмные урны единичных объемов. Нумерация приёмных урн соответствует нумерации случайных величин биномиального распределения.

В начальный момент времени исходная урна содержит два различимых элемента, а приёмные урны пусты.

В первый момент времени из исходной урны выбирают один элемент $n_1=1$ и направляют его в первую приёмную урну с вероятностью $p_1=0,5$ .

Во второй момент времени оставшийся элемент $n_2=1$ исходной урны отправляют во вторую приёмную урну с вероятностью $p_2=0,5$ .

В результате исходная урна пуста, а её два элемента по одному размещены в приёмных урнах. После обработки результатов разбиения исходного множества на два подмножества все элементы из приёмных урн возвращают в исходную урну. На этом один цикл повторных зависимых экспериментов закончен, и урновая модель готова к проведению следующего цикла экспериментов.

Произведение вероятностей попадания по одному произвольному элементу в каждую приёмную урну есть математическое ожидание биномиального распределения.

Изменение характеристик биномиального распределения в окрестности его математического ожидания приведено в таблице 2.

Таблица 2 – Окрестности математического ожидания биномиального распределения настоящей интерпретации 21-го века
Числовые значения первой случайной величины $X_1=n_1$	Числовые значения второй случайной величины $X_2=n_2\| X_1=n_1$	Вероятность распределения	Дисперсия распределения	Математическое ожидание распределения
1	1	0,50	0,75	0,50
2	0	0,25	0,50
0	2	0,25	0,50

Вероятность биномиального распределения как функция двух переменных является симметричной функцией относительно своего математического ожидания.

Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами

Объекты: множество, его подмножества и их элементы как объективная реальность, существующая вне нас и независимо от нас. Биномиальное распределение это:

случайный процесс безвозвратного разделения последовательно во времени $t_1, t_2$ и в пространстве конечного $n$ - множества различимых неупорядоченных элементов на две части $n_1, n_2$ случайных объёмов, сумма которых равна объёму исходного множества: $n_1+ n_2=n, \quad 2\le n<\infty$ ,

разделение множества осуществляют выборками без возвращения (изъятые из множества элементы не возвращают обратно во множество до полного окончания экспериментов),

вероятность попадания одного произвольного элемента множества в каждое из подмножеств принимают за вероятность случайной величины распределения Бернулли с положительным исходом $0\le p_i<1, \quad i=1,2$ ,

результаты испытаний Бернулли неизменны во время проведения разбиения множества и пронормированы $\sum _{i=1}^2 p_i =1$ согласно аксиоматике Колмогорова,
очерёдность следования выборок принимают за очередность следования во времени и нумерацию случайных величин $X_1, X_2$ биномиального распределения,

случайный объём каждой выборки $n_i, \quad i=1,2$ в момент времени $t_i, \quad i=1,2$ принимают за числовое значение соответствующей случайной величины $X_i=n_i, \quad i=1,2$ биномиального распределения,

первая случайная величина биномиального распределения является независимой и может принимать любое случайное значение в пределах от нуля до числового значения исходного множества $X_1=n_1, \quad 0\le n_1\le n<\infty$ ,

вторая случайная величина биномиального распределения принимает числовое значение $n_2$ , равное числу элементов множества оставшееся после изъятия из него первой выборкой случайного числа элементов $n_1: \quad n_2=n-n_1$ ,

результаты каждого разбиения обрабатывают вероятностными методами, определяют технические характеристике всех выборок и принимают их за технические характеристики случайных величин биномиального распределения,

минимально необходимый набор технических характеристик случайных величин и биномиального распределения в целом это: пространство элементарных событий, вероятность , математическое ожидание и дисперсия,

математическое ожидание биномиального распределения имеет место, когда число выборок $k$ равно числу элементов $n$ -множества $k=n$ и численно равно $\frac{n!}{n^n}=\frac{2!}{2^2}=\frac{1}{2}$ .

Сравнительная оценка характеристик биномиальных распределений настоящей и традиционной интерпретаций

Цель сравнительной оценки показать, что биномиальное распределение настоящей интерпретации соответствует, а биномиальное распределение традиционной интерпретации не соответствует современным требованиям аксиоматики Колмогорова.

Несоответствие состоит в том, что, во-первых, биномиальное распределение традиционной интерпретации представлено распределением одной случайной величины, а по своей сути и определению оно должно быть распределением двух случайных величин.

Во-вторых, при неограниченном увеличении числа независимых испытаний ( $n$ ) математическое ожидание ( $np$ ) биномиального распределения традиционной интерпретации устремляется к бесконечности, что недопустимо, поскольку сумма всех вероятностей распределения, включая и его математическое ожидание, в любом распределении обязана быть равной единице (см., например, таблицу 1). Кроме того, математическое ожидание ( $np_1$ ) и дисперсия ( $np_1q_1$ ) первой случайной величины биномиального распределения настоящей интерпретации приняты за математическое ожидание ( $np$ ) и дисперсию ( $npq$ ) биномиального распределения традиционной интерпретации.

Историческая справка ^[1]

Связь с другими распределениями

Если $k>2$ ,то получаем мультиномиальное распределение распределение настоящей интерпретации 21-го века.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5»

Категория: Вероятностные распределения

Биномиальное распределение

Материал из MachineLearning.

Версия 13:01, 20 декабря 2012

Содержание

Определение

Основные свойства

Асимптотические приближения при больших $n$

Приближение Пуассона

Нормальное приближение

Локальная теорема Муавра-Лапласа

Интегральная теорема Муавра-Лапласа

Пример

Литература

Ссылки

Интерпретация 21-го века

Биномиальная схема повторных циклов случайных зависимых экспериментов

Биномиальное распределение — совместное распределение двух случайных величин ^[1]

Характер зависимости случайных величин в каждом цикле экспериментов:

Характеристики случайных величин биномиального распределения:

Характеристики биномиального распределения:

Математическое ожидание биномиального распределения

Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами

Сравнительная оценка характеристик биномиальных распределений настоящей и традиционной интерпретаций

Связь с другими распределениями

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты

@@ Строка 120: / Строка 120: @@
 *[http://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%BD%D0%BE%D0%BC%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5 Биномиальное распределение] (Википедия)
 *[http://en.wikipedia.org/wiki/Binomial_distribution Binomial distribution] (Wikipedia)
+== Интерпретация 21-го века ==
+{|border=1 align="center"
+|+Таблица 1 – Характеристики биномиального распределения интерпретации 21-го века
+| Пространство элементарных событий
+| <tex>\sum_{i=1}^2\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})</tex>
+|-
+|Вероятность
+|<tex>\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1}p_2^{n_2}</tex>
+|-
+| Максимальная вероятность
+(при математическом ожидании
+распределения)
+|<tex> \left(\frac{n!}{n_i!n_2!}p_1^{n_1}p_2^{n_2}\right)_{max}= \frac{1}{2}</tex>
+|-
+| Математическое ожидание
+(как максимальное произведение
+математических ожиданий
+случайных величин)
+|<tex>\left(\prod_{i=1}^2E(t_i, X_i=n_i \mid t_{i-1},X_{i-1})\right)_{max}=\frac{1}{2}</tex>
+|-
+| Дисперсия
+|<tex>\sum_{i=1}^2D(t_i,X_i \mid t_{i-1},X_{i-1})=\sum_{i=1}^2(n-n_{i-1})p_iq_i</tex>
+|-
+| Максимальная дисперсия
+(при математическом ожидании
+распределения)
+|<tex>D(X_1,X_2|X_1)_{max}=\left(\sum_{i-1}^2(n-n_{i-1})p_iq_i \right)_{max}=\frac{3}{4}</tex>
+|-
+|Ковариационная матрица
+|<tex>B=\| b_{ij} \|</tex>, где :<tex>\rho _{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j\end{cases} </tex>
+|-
+|Корреляционная матрица
+|<tex>P=\| \rho_{ij} \|</tex>, где
+:<tex>\rho_{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j\end{cases}</tex>
+|-
+|<tex>\chi^2</tex> - критерий
+|<tex> \chi^2=\sum_{i=1}^2 [X_i-(n -n_{i-1})p_i^{(0)}]^2/(n -n_{i-1})p_i^{(0)}=</tex>
+<tex>=-n+\sum_{i=1}^2X_i^2 /(n-n_{i-1})p_i^{(0)}</tex>
+|}
+==Биномиальная схема повторных циклов случайных зависимых экспериментов==
+Каждый цикл экспериментов осуществляют '''методом выбора без возвращения''' в дискретной временной последовательности
+::<tex>t_1, t_2.</tex>
+Каждая из случайных величин распределения
+::<tex>X_i=n_i \mid X_{i-1}=n_{i-1}</tex>
+это <tex>n_i</tex> наступлений одного события
+::<tex>x_i,  i =1,2</tex>
+в <tex>i</tex> - ый момент времени при условии, что в <tex>(i-1)</tex> - ый момент произошло <tex>n_{i-1}</tex> наступлений предшествующего события <tex>x_{i-1}</tex>, &mdash;
+[[ распределение Бернулли | распределения Бернулли]] с успехом, вероятности которых <tex>p_i</tex> нормированы
+::<tex>p_1+p_2=1</tex>
+и неизменны во время проведения экспериментов.
+Если в каждом цикле экспериментов вероятность наступления события <tex>x_i</tex> равна <tex>p_i</tex>, то биномиальная вероятность равна вероятности того, что при <tex>n</tex> экспериментах события <tex>x_1, x_2</tex> наступят <tex>n_1,  n_2</tex> раз соответственно.
+'''Случайная величина биномиального распределения''' в соответствующей точке дискретной временной последовательности <tex>t_1, t_2</tex> имеет:
+пространство элементарных событий
+::<tex>\Omega_i(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})= [0\le n_i \le n-n_{i-1}], </tex>
+вероятность
+::<tex>P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})={n-n_{i-1}\choose n_i}p_i^{n_i},</tex>
+математическое ожидание
+::<tex>E(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=( n-n_{i-1})p_i</tex>
+и дисперсию
+::<tex>D(t_i,X_i \mid t_{i-},X_{i-1})=( n -n_{i-1})p_iq_i, \quad q_i=1-p_i .</tex>
+'''Пространство элементарных событий биномиального распределения''' есть сумма точечных пространств элементарных событий его случайных величин, образующих дискретную последовательность точек <tex> t_1,  t_2 </tex> цикла, а ''вероятность биномиального распределения'' &mdash; произведение вероятностей его случайных величин.
+==Биномиальное распределение &mdash; совместное распределение '''двух''' случайных величин <ref> http://ru.wikiznanie.org/wiki/  Биномиальное распределение, Настоящая интерпретация   21-го века. </ref>==
+::<tex>\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1! n_2!}p_1^{n_1} p_2^{n_2},\qquad \frac{n!}{n_1!n_2!}={n\choose n_1,n_2}= {n \choose n_1}={n\choose n_2}, </tex>
+::<tex>2\le k \le n <\infty,  \qquad n_1+n _2=n, \qquad p_1+p_2=1,</tex>
+определённых на точечных пространствах элементарных событий
+::<tex>\Omega_1,  \Omega _2</tex>
+и принимающих в дискретные последовательные моменты времени
+::<tex>t_1,  t_2, \quad  t_i<t_{i+1}</tex>
+целые неотрицательные значения
+::<tex>n_1, n_2,</tex>
+взаимосвязанные условием
+::<tex>n_1 +n_2=n,</tex>
+согласно которому
+::<tex>X_2=n_2 \mid X_1=n_1</tex>
+если в первый момент времени <tex>t_1</tex> первая случайная величина <tex>X_1</tex> приняла значение
+::<tex>n_1, \quad  0\le n_1\le n,</tex>
+то во второй момент времени <tex>t_2</tex>вторая случайная величина
+<tex>X _2</tex> принимает значение
+::<tex> n _2, \quad  0\le n_2\le n- n_1.</tex>
+==Характер зависимости случайных величин в каждом цикле экспериментов:==
+*только первая случайная величина является независимой, а вторая случайная величина зависима от первой;
+* если первая случайная величина в первый момент времени приняла своё максимально возможное значение, равное <tex>X_1=n</tex>, то вторая случайная величина во второй момент времени обязана принять своё минимальное (нулевое) значение <tex>X_2=n_2=0</tex> в противном случае не будет выполнено условие суммирования числовых значений случайных величин распределения, согласно которому <tex>n_1+n _2=n</tex>;
+* если первая случайная величина в первый момент времени приняла своё минимальное (нулевое) значение <tex>X_1=n_1=0</tex>, то вторая случайная величина во второй момент времени обязана принять своё максимальное значение <tex>X_2=n_2=n</tex> в противном случае не будет выполнено условие <tex>n_1+n _2=n</tex>.
+==Характеристики случайных величин биномиального распределения:==
+пространство элементарных событий
+::<tex>\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=[0 \le n_i \le n-n_{i-1}],</tex>
+вероятность
+::<tex>P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})={n-n_{i-1}\choose n_i}p_i^{n_i},</tex>
+математическое ожидание
+::<tex>E(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=(n-n_{i-1})p_i,</tex>
+Дисперсия
+::<tex>D(t_i,X_i \mid t_{i-1},X_{i-1})=(n -n_{i-1})p_iq_i, \quad q_i=1-p_i,</tex>
+производящая
+::<tex>A(s_i)=(1+p_is_i)^{n-n_{i-1}}</tex>
+и характеристическая
+::<tex>f(t_i)=(1+p_ie^{jt_i})^{n-n_{i-1}}</tex>
+функции.
+==Характеристики биномиального распределения:==
+пространство элементарных событий
+::<tex>\sum_{i=1}^2\Omega_i(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1}), </tex>
+расположенное в точках <tex>t_1,  t_2</tex> временной последовательности,
+вероятность
+::<tex>\prod_{i=1}^2P(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})=\frac{n!}{n_1!n_2!}p_1^{n_1}p_2^{n_2},</tex>
+дисперсия
+::<tex>\sum_{i=1}^2D(t_i,X_i \mid t_{i-1},X_{i-1})=\sum_{i=1}^2(n-n_{i-1})p_iq_i,</tex>
+ковариационная матрица <tex>B=\| b_{ij} \|</tex>, где
+::<tex>b_{ij} = \begin{cases} (n-n_{i-1})p_iq_i, & i=j,\\0, & i \not= j,\end{cases}</tex>
+корреляционная матрица <tex>P=\| \rho_{ij} \|</tex>, где
+::<tex>\rho _{ij} = \begin{cases} 1, & i=j,\\0, & i \not= j,\end{cases}</tex>
+::<tex>\chi^2</tex> - квадрат критерий для полиномиально распределенных случайных величин
+::<tex>\chi^2=\sum_{i=1}^2 [X_i-(n -n_{i-1})p_i^{(0)}]^2/(n -n_{i-1})p_i^{(0)}= </tex>
+::<tex>=-n+\sum_{i=1}^2X_i^2 /(n-n_{i-1})p_i^{(0)}.</tex>
+'''Урновая модель биномиального распределения''' содержит одну исходную урну и две приёмные урны. В начальный момент времени исходная урна содержит <tex>n</tex>- множество различимых неупорядоченных элементов, а приёмные урны пусты.
+Объем каждой из них не менее объёма исходной урны. Нумерация приёмных урн соответствует нумерации случайных величин биномиального распределения.
+Первая [[выборка]]
+::<tex>n_1,\quad  0\le n_1\le n</tex>
+в первый момент времени направляется в первую приёмную урну с вероятностью <tex>p_1</tex> каждого элемента.
+Во второй момент времени все оставшиеся <tex>n-n_1</tex> элементы исходной урны, образующие вторую выборку
+::<tex>n_2,\quad  0\le n-n_1\le n,</tex>
+направляются во вторую приёмную урну с вероятностью <tex>p_2</tex> каждого элемента.
+В результате исходная урна пуста, а все её элементы размещены в приёмных урнах.
+После обработки результатов разбиения множества на подмножества элементы возвращают на прежнее место, и урновая модель готова к проведению очередного цикла зависимых экспериментов.
+Произведение вероятностей попадания <tex>n_1, n_2</tex> элементов в две приёмные урны есть '''биномиальное распределение. '''
+==Математическое ожидание биномиального распределения==
+получают одним из двух способов: как максимум произведения математических ожиданий его случайных величин, или как максимум вероятности распределения.
+'''Необходимые'''
+::<tex>k=n, \qquad n_i=1,  \qquad  0<p_i<1,</tex>
+'''и достаточные'''
+::<tex>p_1=p_2=2^{-1}</tex>
+'''условия''' получения математического ожидания биномиального распределения.
+Математическое ожидание
+::<tex>\left(\prod_{i=1}^2E(t_i,X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})\right)_{max}=\left(\prod_{i=1}^2(n-n_{i-1})p_i\right)_{max}=\frac{n!}{n^n}=\frac{1}{2},</tex>
+максимальная вероятность
+::<tex>\left(\prod_{i=1}^2P(t_i, X_i=n_i \mid t_{i-1},X_{i-1}=n_{i-1})\right)_{max}=\left(\frac{n!}{n_i!n_2!}p_1^{n_1}p_2^{n_2}\right)_{max}=\frac{n!}{n^n}= \frac{1}{2}</tex>
+равна математическому ожиданию,
+максимальная дисперсия
+::<tex>D(X_1,X_2|X_1)_{max}=\left(\sum_{i-1}^2(n-n_{i-1})p_iq_i \right)_{max}=\frac{n^2-1}{2n}=\frac{3}{4}.</tex>
+Пространство элементарных событий биномиального распределения при получении его математического ожидания
+::<tex>\Omega(t_1, X_1=n_1=1 \mid t_2,X_2=n_2=1)</tex>
+расположено в точках <tex>t_1, t_2</tex> временной последовательности.
+'''Урновая модель получения математического ожидания биномиального распределения''' содержит одну исходную урну и две приёмные урны единичных объемов. Нумерация приёмных урн соответствует нумерации случайных величин биномиального распределения.
+В начальный момент времени исходная урна содержит два различимых элемента, а приёмные урны пусты.
+В первый момент времени из исходной урны выбирают один элемент <tex>n_1=1</tex> и направляют его в первую приёмную урну с вероятностью <tex>p_1=0,5</tex> .
+Во второй момент времени оставшийся элемент <tex>n_2=1</tex> исходной урны отправляют во вторую приёмную урну с вероятностью <tex>p_2=0,5</tex>.
+В результате исходная урна пуста, а её два элемента по одному размещены в приёмных урнах. После обработки результатов разбиения исходного множества на два подмножества все элементы из приёмных урн возвращают в исходную урну. На этом один цикл повторных зависимых экспериментов закончен, и урновая модель готова к проведению следующего цикла экспериментов.
+Произведение вероятностей попадания по одному произвольному элементу в каждую приёмную урну есть '''математическое ожидание биномиального распределения. '''
+'''Изменение характеристик биномиального распределения в окрестности его математического ожидания''' приведено в таблице 2.
+{|border=1 align="center"
+|+Таблица 2 – Окрестности математического ожидания биномиального распределения настоящей интерпретации 21-го века
+| Числовые значения первой случайной величины <tex>X_1=n_1</tex>
+| Числовые значения второй случайной величины <tex>X_2=n_2| X_1=n_1</tex>
+|Вероятность распределения
+|Дисперсия распределения
+|Математическое ожидание распределения
+|-
+|1
+|1
+|0,50
+|0,75
+|0,50
+|-
+|2
+|0
+|0,25
+|0,50
+|rowspan=2 |
+|-
+|0
+|2
+|0,25
+|0,50
+|}
+Вероятность биномиального распределения как функция двух переменных является симметричной функцией относительно своего математического ожидания.
+==Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами==
+[[Объект | Объекты]]: [[множество | множество]], его [[подмножества | подмножества]] и их [[элемент | элементы]] как объективная [[реальность | реальность]], существующая вне нас и независимо от нас.
+Биномиальное распределение это:
+*  [[случайный процесс | случайный процесс ]] безвозвратного разделения последовательно во времени <tex> t_1, t_2 </tex> и в пространстве конечного <tex> n</tex>- множества различимых неупорядоченных элементов на две части <tex> n_1, n_2 </tex> случайных объёмов, сумма которых равна объёму исходного множества: <tex> n_1+ n_2=n, \quad 2\le n<\infty </tex>,
+* разделение множества осуществляют [[выборка | выборками]] без возвращения (изъятые из множества элементы не возвращают обратно во множество до полного окончания экспериментов),
+* вероятность попадания одного произвольного элемента множества в каждое из подмножеств принимают за вероятность случайной величины [[ распределение Бернулли |распределения Бернулли]] с положительным исходом <tex> 0\le p_i<1, \quad i=1,2</tex>,
+* результаты испытаний Бернулли неизменны во время проведения разбиения множества и пронормированы <tex> \sum _{i=1}^2 p_i =1</tex> согласно [[аксиоматика Колмогорова | аксиоматике Колмогорова]],
+* очерёдность следования выборок принимают за очередность следования во времени и нумерацию случайных величин <tex> X_1, X_2 </tex> биномиального распределения,
+*случайный объём каждой выборки <tex> n_i, \quad i=1,2</tex> в момент времени <tex> t_i, \quad i=1,2</tex> принимают за числовое значение соответствующей случайной величины <tex> X_i=n_i, \quad i=1,2</tex> биномиального распределения,
+*  первая случайная величина биномиального распределения является независимой и может принимать любое случайное значение в пределах от нуля до числового значения исходного множества <tex> X_1=n_1, \quad  0\le n_1\le n<\infty </tex>,
+* вторая случайная величина биномиального распределения принимает числовое значение <tex> n_2 </tex>, равное числу элементов множества оставшееся после изъятия из него первой выборкой случайного числа элементов <tex> n_1: \quad  n_2=n-n_1 </tex>,
+* результаты каждого разбиения обрабатывают вероятностными методами, определяют технические характеристике всех выборок и принимают их за технические характеристики случайных величин биномиального распределения,
+* минимально необходимый набор технических характеристик случайных величин и биномиального распределения в целом это: [[пространство элементарных событий | пространство элементарных событий]], [[ вероятность ]], [[математическое ожидание |математическое ожидание]] и [[дисперсия |дисперсия]],
+* математическое ожидание биномиального распределения имеет место, когда число выборок <tex>k</tex> равно числу элементов <tex> n</tex>-множества <tex> k=n</tex> и численно равно <tex> \frac{n!}{n^n}=\frac{2!}{2^2}=\frac{1}{2} </tex>.
+==Сравнительная оценка характеристик биномиальных распределений настоящей и традиционной интерпретаций==
+Цель сравнительной оценки показать, что биномиальное распределение настоящей интерпретации соответствует, а биномиальное распределение традиционной интерпретации не соответствует современным требованиям аксиоматики Колмогорова.
+Несоответствие состоит в том, что, во-первых, биномиальное распределение традиционной интерпретации представлено распределением одной случайной величины, а по своей сути и определению оно должно быть распределением двух случайных величин.
+Во-вторых, при неограниченном увеличении числа независимых испытаний ( <tex>n </tex>) математическое ожидание (<tex>np </tex>) биномиального распределения традиционной интерпретации устремляется к бесконечности, что недопустимо, поскольку сумма всех вероятностей распределения, включая и его математическое ожидание, в любом распределении обязана быть равной единице (см., например, таблицу 1). Кроме того, математическое ожидание (<tex>np_1 </tex>) и дисперсия (<tex>np_1q_1 </tex>) первой случайной величины биномиального распределения настоящей интерпретации приняты за математическое ожидание (<tex>np </tex>) и дисперсию (<tex>npq</tex>) биномиального распределения традиционной интерпретации.
+Историческая справка <ref> http://ru.wikiznanie.org/wiki/  Биномиальное распределение, Настоящая интерпретация   21-го века, раздел Историческая  справка</ref>
+==Связь с другими распределениями==
+Если <tex>k>2</tex>,то получаем [[мультиномиальное распределение]] распределение настоящей интерпретации 21-го века.
 [[Категория:Вероятностные распределения]]

Биномиальное распределение

Материал из MachineLearning.

Версия 13:01, 20 декабря 2012

Содержание

Определение

Основные свойства

Асимптотические приближения при больших

Приближение Пуассона

Нормальное приближение

Локальная теорема Муавра-Лапласа

Интегральная теорема Муавра-Лапласа

Пример

Литература

Ссылки

Интерпретация 21-го века

Биномиальная схема повторных циклов случайных зависимых экспериментов

Биномиальное распределение — совместное распределение двух случайных величин [1]

Характер зависимости случайных величин в каждом цикле экспериментов:

Характеристики случайных величин биномиального распределения:

Характеристики биномиального распределения:

Математическое ожидание биномиального распределения

Биномиальное распределение как процесс выполнения взаимосвязанных действий над объектами

Сравнительная оценка характеристик биномиальных распределений настоящей и традиционной интерпретаций

Связь с другими распределениями

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты

Асимптотические приближения при больших $n$

Биномиальное распределение — совместное распределение двух случайных величин ^[1]