Сравнение временных рядов при авторегрессионном прогнозе (пример)

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(→Вычислительный эксперимент)
(→Вычислительный эксперимент)
Строка 71: Строка 71:
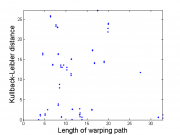
'''3)''' строится зависимость расстояния между последовательностями в пространстве параметров:
'''3)''' строится зависимость расстояния между последовательностями в пространстве параметров:
-
 
+
[[Изображение:KL WarpingPath Distance.png|thumb|left]]
<center><tex> D_{KL} \left( \mathbf{x}(n), \mathbf{x}(m) \right)= D_{KL}\left(p(w), q(w) \right) = \sum\limits_{w\in \mathcal{W}} p(w) \ln \frac{p(w)}{q(w)} </tex>,</center> где <tex>p(w),q(w)</tex> - плотности распределений случайных величины из <tex>N(\mathbf{w}(n),A(n))</tex> и <tex>N(\mathbf{w}(m),A(m))</tex> соотвественно,
<center><tex> D_{KL} \left( \mathbf{x}(n), \mathbf{x}(m) \right)= D_{KL}\left(p(w), q(w) \right) = \sum\limits_{w\in \mathcal{W}} p(w) \ln \frac{p(w)}{q(w)} </tex>,</center> где <tex>p(w),q(w)</tex> - плотности распределений случайных величины из <tex>N(\mathbf{w}(n),A(n))</tex> и <tex>N(\mathbf{w}(m),A(m))</tex> соотвественно,
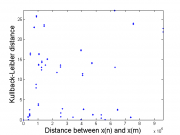
и расстояний в пространстве значений:
и расстояний в пространстве значений:
<center><tex>Dintance \left( \mathbf{x}(n), \mathbf{x}(m) \right)=\sum_{t=1}^{24}\left( x_t(n)-x_t(m) \right)^2 </tex></center>
<center><tex>Dintance \left( \mathbf{x}(n), \mathbf{x}(m) \right)=\sum_{t=1}^{24}\left( x_t(n)-x_t(m) \right)^2 </tex></center>
 +
[[Изображение:KL SSE Distance.png|thumb|left]]
== Исходный код ==
== Исходный код ==

Версия 23:02, 20 декабря 2010

Содержание

Аннотация

Временным рядом называется последовательность упорядоченных по времени значений некоторой вещественной переменной $\mathbf{x}=\{x_{t}\}_{t=1}^T\in\mathbb{R}^T$. Элемент последовательности называется отсчетом временного ряда.

Задача авторегрессионного прогноза заключается в нахождении модели $f(\mathbf{x}, \mathbf{w})$, где $\mathbf{w}\in\mathbb{R}^M$ вектор параметров модели, которая наилучшим образом приближает следущее значение временного ряда $x_{T+1}:\widehat{x}_{T+1}=f(\mathbf{x}, \mathbf{w})$. Свертка временного ряда возникает в случае существования на множестве подпоследовательностей временного ряда некоторого инварианта. Примером инварианта является период временного ряда, который физически может означать сезонность в данных. При этом построенная модель должна учитывать наличие инварианта и сохранять данное свойство для ряда прогнозов: $\{\widehat{x}_{t}\}_{t=1}^T\in\mathbb{R}^T$.

Постановка задачи

Пусть задан временной ряд $\mathbf{x}=\{x_{t}\}_{t=1}^T\in\mathbb{R}^T$. Предполагается, что отсчеты t=1,\dots, T были сделаны через равные промежутки времени, и период временного ряда равен $p$, при этом $ {T}+1=p\cdot{n}$, где n\in\mathbb{N}. Задана модель $\mathbf{x}=f(\mathbf{x}, w)+\epsilon$,где случайная величина \mathbf{\varepsilon} имеет нормальное распределение \mathbf{\varepsilon} \in N(0, \sigma^2). Вектор параметров модели \mathbf{w} рассматривается как многомерная случайная величина. Пусть плотность распределения параметров имеет вид многомерного нормального распределения N(\mathbf{0}, A) с матрицей ковариации A. Модель некоторым образом учитывает период временного ряда. Предполагается, модель временного ряда может меняться с течением времени, т.е. для разных подпоследовательностей длины p оптимальные параметры модели $\mathbf{x}=f(\mathbf{x}, w)+\epsilon$ будут отличаться. Расстояние между различными подпоследовательностями x_{n_1\cdot{p}+1},\dots,x_{(n_1+1)\cdot{p}} и x_{n_2\cdot{p}+1},\dots,x_{(n_2+1)\cdot{p}} измеряется как сумма квадратов отклонений:

SSE=\sum_{i=1}^p{(x_{n_2{p}+i}-x_{n_1{p}+i})^2}
.

Расстояние между параметрами модели $\mathbf{x}=f(\mathbf{x}, w)+\epsilon$, настроенной на разных подпоследовательностях, можно измерить как расстояние Кульбака-Лейблера между функциями распределения 2-ух случайных величин {p(x)},{q(x)}:

D_{KL}(p, q) = \sum\limits_{x\in \mathcal{X}} p(x) \ln \frac{p(x)}{q(x)}.

Требуется исследовать зависимость расстояния между параметрами модели $\mathbf{x}=f(\mathbf{x}, w)+\epsilon$ от расстояния между подпоследовательностями, на которых эти параметры были настроены.

Алгоритм

Для настройки параметров модели f(\mathbf{x}, \mathbf{w})+\epsilon используется связный байесовский вывод

\ln p(D|\beta, A)=-\frac{1}{2}\ln|A|-\frac{N}{2}\ln2\pi+\frac{N}{2}\ln\beta-S(\mathbf{w_0})-\frac{1}{2}\ln|H|,

где S(\mathbf{w})=\frac{1}{2}\mathbf{w}^TA\mathbf{w}+\beta E_D — функция ошибки,

H=-\nabla\nabla S(\mathbf{w})|_{\mathbf{w}=\mathbf{w_0}} — матрица Гессе функции ошибок,

E_D=\frac{1}{2}\sum^n_{i=1}(\widehat{x_i}-x_i)^2 — функция ошибки в пространстве данных.

Настройка параметрической регрессионной модели происходит в 2 этапа, сначала настраиваются параметры \mathbf{w} при фиксированных гиперпараметрах \beta, A, затем при вычисленных значениях параметров функция правдоподобия \ln p(D|\beta, A) оптимизируется по гиперпараметрам. Процедура повторяется, пока настраиваемые параметры не стабилизируется.

Для простоты вычислений, считаем, что A имеет диагональный вид:

A=\left( \begin{array}{cccc} \alpha_{1} & 0 & \dots & 0\\ 0 & \alpha_2 & \dots & 0 \\ \vdots & \vdots & \ddots & 0\\ 0 & \dots & 0 & \alpha_M\\ \end{array} \right). .

Вычислительный эксперимент

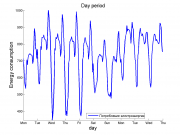
Вычислительный эксперимент проводился на реальных данных. Использовались временные ряды потребления электроэнергии в некотором регионе с отсчетами 1 час, период ряда равен p=24.

Эксперимент состоит из этапов:

1) из множества порождающих моделей:

f_1(x) = x; f_2(x) = \sin(x); f_3(x) = \cos(x); f_4(x) = \exp(x); f_5(x) = \ln(x); f_6(x) = \tan(x);

была построена их суперпозиция, описывающая потребление электроэнергии за сутки: $$\widehat{x}_{pn+t}=w_1\cdot{\sqrt{t}}+w_2\cdot{\exp(-t)}+w_3\cdot{\exp(-24*t)}+w_4\cdot \exp\left(w_5\cdot{\sin(t^4)} \right)+w_6\cdot \exp \left( w_7\cdot cos(24*t^{2,5})\right)+$$

$$+w_8\cdot \exp\left(w_9\cdot sin(t^{-0,5}) \right)+w_{10}\cdot cos(t)+w_{11}\cdot cos(\frac{2}{15}\cdot t+\frac{1}{3}))+w_{12}\cdot t\cdot cos(t^3).$$

2) модель настраивается на подпоследовательности

\mathbf{x}(n)=\{x_{pn+1},\dots,x_{pn+24}\},

где n - номер суток. В результате получаем набор оптимальных параметров и гиперпараметров модели, оптимальных для данной подпоследовательности:

\mathbf{w}(n), A(n), \beta(n)
.

3) строится зависимость расстояния между последовательностями в пространстве параметров:

D_{KL} \left( \mathbf{x}(n), \mathbf{x}(m) \right)= D_{KL}\left(p(w), q(w) \right) = \sum\limits_{w\in \mathcal{W}} p(w) \ln \frac{p(w)}{q(w)} ,
где p(w),q(w) - плотности распределений случайных величины из N(\mathbf{w}(n),A(n)) и N(\mathbf{w}(m),A(m)) соотвественно,

и расстояний в пространстве значений:

Dintance \left( \mathbf{x}(n), \mathbf{x}(m) \right)=\sum_{t=1}^{24}\left( x_t(n)-x_t(m) \right)^2

Исходный код

Смотри также

Литература

  1. Стрижов В.В, Пташко Г.О. Построение инвариантов на множестве временных рядов путем динамической свертки свободной переменной. — ВЦ РАН, 2009.
  2. Стрижов В.В Методы выбора регрессионных моделей. — ВЦ РАН, 2010.
Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A1%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B2%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D1%8B%D1%85_%D1%80%D1%8F%D0%B4%D0%BE%D0%B2_%D0%BF%D1%80%D0%B8_%D0%B0%D0%B2%D1%82%D0%BE%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%BE%D0%BD%D0%BD%D0%BE%D0%BC_%D0%BF%D1%80%D0%BE%D0%B3%D0%BD%D0%BE%D0%B7%D0%B5_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»
Личные инструменты