Распределение Фишера

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м
Текущая версия (21:22, 14 февраля 2020) (править) (отменить)
(Fix tex)
 
Строка 6: Строка 6:
parameters =<tex>d_1>0,\ d_2>0</tex> - числа степеней свободы |
parameters =<tex>d_1>0,\ d_2>0</tex> - числа степеней свободы |
support =<tex>x \in [0; +\infty)\!</tex>|
support =<tex>x \in [0; +\infty)\!</tex>|
-
pdf =<tex>\frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}}
+
pdf =<tex>\frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}}{(d_1\,x+d_2)^{d_1+d_2}}}}{x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}</tex>|
-
{(d_1\,x+d_2)^{d_1+d_2}}}}
+
-
{x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}\!</tex>|
+
cdf =<tex>I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!</tex>|
cdf =<tex>I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!</tex>|
mean =<tex>\frac{d_2}{d_2-2}\!</tex>, если <tex>d_2 > 2</tex>|
mean =<tex>\frac{d_2}{d_2-2}\!</tex>, если <tex>d_2 > 2</tex>|

Текущая версия

Распределение Фишера
Плотность вероятности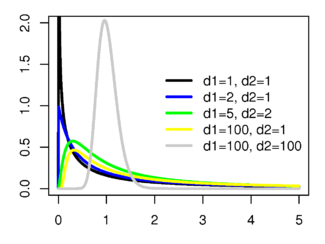
Функция распределения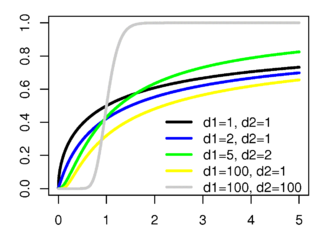
Параметры d_1>0,\ d_2>0 - числа степеней свободы
Носитель x \in [0; +\infty)\!
Плотность вероятности \frac{\sqrt{\frac{(d_1\,x)^{d_1}\,\,d_2^{d_2}}{(d_1\,x+d_2)^{d_1+d_2}}}}{x\,\mathrm{B}\!\left(\frac{d_1}{2},\frac{d_2}{2}\right)}
Функция распределения I_{\frac{d_1 x}{d_1 x + d_2}}(d_1/2, d_2/2)\!
Математическое ожидание \frac{d_2}{d_2-2}\!, если d_2 > 2
Медиана
Мода \frac{d_1-2}{d_1}\;\frac{d_2}{d_2+2}\!, если d_1 > 2
Дисперсия \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!, если d_2 > 4
Коэффициент асимметрии \frac{(2 d_1 + d_2 - 2) \sqrt{8 (d_2-4)}}{(d_2-6) \sqrt{d_1 (d_1 + d_2 -2)}}\!,
если d_2 > 6
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов '
Характеристическая функция


Распределе́ние Фи́шера в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений.

Содержание

Определение

Пусть Y_1,Y_2 — две независимые случайные величины, имеющие распределение хи-квадрат: Y_i \sim \chi^2(d_i), где d_i \in \mathbb{N},\; i=1,2. Тогда распределение случайной величины

F = \frac{Y_1/d_1}{Y_2/d_2},

называется распределением Фишера со степенями свободы d_1 и d_2. Пишут F \sim \mathrm{F}(d_1,d_2).

Моменты

Математическое ожидание и дисперсия случайной величины, имеющей распределение Фишера, имеют вид:

\mathbb{M}[F] = \frac{d_2}{d_2 - 2}, если d_2 > 2,
\mathrm{D}[F] = \frac{2\,d_2^2\,(d_1+d_2-2)}{d_1 (d_2-2)^2 (d_2-4)}\!, если d_2 > 4.

Свойства распределения Фишера

  • Если F \sim \mathrm{F}(d_1,d_2), то
\frac{1}{F} \sim \mathrm{F}(d_2, d_1).
  • Распределение Фишера сходится к единице: если F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2), то
F_{d_1,d_2} \to \delta(x-1) по распределению при d_1,d_2 \to \infty,

где \delta(x-1) — дельта-функция в единице, то есть распределение случайной величины-константы X \equiv 1.

Связь с другими распределениями

  • Если F_{d_1,d_2} \sim \mathrm{F}(d_1,d_2), то случайные величины d_1 F_{d_1,d_2} сходятся по распределению к \chi^2(d_1) при d_2 \to \infty.


Данная статья является непроверенным учебным заданием.
Студент: Участник:Bogdan
Преподаватель: Участник:Vokov
Срок: 31 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.


Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%A4%D0%B8%D1%88%D0%B5%D1%80%D0%B0»