Распределение хи-квадрат

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

**Распределение хи-квадрат**
Плотность вероятности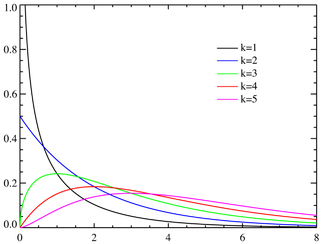 k - число степеней свободы
Функция распределения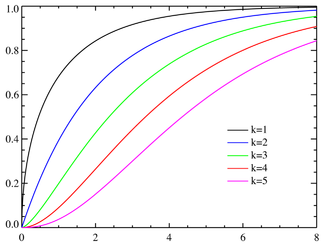 k - число степеней свободы
Параметры	$n > 0\,$ число степеней свободы
Носитель	$x \in [0; +\infty)\,$
Плотность вероятности	$\frac{(1/2)^{n/2}}{\Gamma(n/2)} x^{n/2 - 1} e^{-x/2}\,$
Функция распределения	$\frac{\gamma(n/2,x/2)}{\Gamma(n/2)}\,$
Математическое ожидание	$n\,$
Медиана	примерно $n-2/3\,$
Мода	$n-2\,$ если $n\geq 2\,$
Дисперсия	$2\,n\,$
Коэффициент асимметрии	$\sqrt{8/n}\,$
Коэффициент эксцесса	$12/n\,$
Информационная энтропия	$\frac{n}{2}\!+\!\ln\left[2\Gamma\left({n \over 2}\right)\right]\!+\!\left(1\!-\!\frac{n}{2}\right)\psi\left(\frac{n}{2}\right)$ $\!\psi(x) = \Gamma'(x) / \Gamma(x).$
Производящая функция моментов	$(1-2\,t)^{-n/2}$ , если $2\,t<1\,$
Характеристическая функция	$(1-2\,i\,t)^{-n/2}\,$

Распределение $\!\chi^2$ (хи-квадрат) с n степенями свободы — это распределение суммы квадратов n независимых стандартных нормальных случайных величин.

Определение

Пусть $X_1, \ldots, X_n$ — совместно независимые стандартные нормальные случайные величины, то есть: $X_i \sim N(0,1)$ . Тогда случайная величина

$Y = X_1^2 + \cdots + X_n^2$

имеет распределение хи-квадрат с n степенями свободы, обозначаемое $\!\chi^2(n)$ .

Замечание. Распределение хи-квадрат является частным случаем Гамма распределения:

$\chi^2(n) \equiv \Gamma\left({n \over 2}, {2}\right)$ .

Следовательно, плотность распределения хи-квадрат имеет вид

$f_{\chi^2(n)}(x) = \frac{(1/2)^{n \over 2}}{\Gamma\left({n \over 2}\right)}\, x^{{n \over 2} - 1}\, e^{-\frac{x}{2}}$ ,

а его функция распределения

$F_{\chi^2(n)}(x) = \frac{\gamma\left({n \over 2}, {x \over 2}\right)}{\Gamma\left({n \over 2}\right)}$ ,

где $\!\Gamma$ и $\!\gamma$ обозначают соответственно полную и неполную гамма-функции.

Свойства распределения хи-квадрат

Распределение хи-квадрат устойчиво относительно суммирования. Если $\!Y_1, Y_2$ независимы, и $\!Y_1 \sim \chi^2(n_1)$ , а $\!Y_2 \sim \chi^2(n_2)$ , то

$Y_1 + Y_2 \sim \chi^2(n_1 + n_2)$ .

Из определения легко получить моменты распределения хи-квадрат. Если $Y \sim \chi^2(n)$ , то

$\mathbb{E}[Y] = n$ ,

$\!\mathrm{D}[Y] = 2n$ .

В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины $Y \sim \chi^2(n)$ может быть приближено нормальным $Y \approx N( n, 2n )$ . Более точно

$\frac{Y-n}{\sqrt{2n}} \to N(0,1)$ по распределению при $n \to \infty$ .

Связь с другими распределениями

Если $X_1 ,\ldots , X_n$ независимые нормальные случайные величины, то есть: $X_i \sim N(\mu,\sigma^2),\; i=1,\ldots, n$ , то случайная величина

$Y = \sum_{i=1}^n \left(\frac{X_i - \mu}{\sigma}\right)^2$

имеет распределение хи-квадрат.

Если $\!n=2$ , то распределение хи-квадрат совпадает с экспоненциальным распределением:

$\chi^2(2) \equiv \mathrm{Exp}(1/2)$ .

Если $Y_1 \sim \chi^2(n_1)$ и $Y_2 \sim \chi^2(n_2)$ , то случайная величина

$F = \frac{Y_1/n_1}{Y_2 / n_2}$

имеет распределение Фишера со степенями свободы $\!(n_1,n_2)$ .

Данная статья является непроверенным учебным заданием.

Студент: Участник:Bogdan

Преподаватель: Участник:Vokov

Срок: 31 декабря 2009

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82»

Категории: Вероятностные распределения | Непроверенные учебные задания

@@ Строка 2: / Строка 2: @@
   name       =Распределение хи-квадрат|
   type       =Плотность|
-  pdf_image  =[[Файл:chi-square_distributionPDF.png|325px]] <br /><small>k - число степеней свободы</small>|
+  pdf_image  =[[Изображение:chi-square_distributionPDF.png|325px]] <br /><small>k - число степеней свободы</small>|
-  cdf_image  =[[Файл:chi-square_distributionCDF.png|325px]] <br /><small>k - число степеней свободы</small>|
+  cdf_image  =[[Изображение:chi-square_distributionCDF.png|325px]] <br /><small>k - число степеней свободы</small>|
   parameters =<tex>n > 0\,</tex> число степеней свободы|
   support    =<tex>x \in [0; +\infty)\,</tex>|
@@ Строка 57: / Строка 57: @@
 : <tex>F = \frac{Y_1/n_1}{Y_2 / n_2}</tex>
 имеет [[распределение Фишера]] со степенями свободы <tex>\!(n_1,n_2)</tex>.
+[[Категория:Вероятностные распределения]]
+{{Задание|Bogdan|Vokov|31 декабря 2009}}

Распределение хи-квадрат

Материал из MachineLearning.

Текущая версия

Определение

Свойства распределения хи-квадрат

Связь с другими распределениями

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты