Оценка параметров смеси моделей

Материал из MachineLearning.

(Различия между версиями)

Текущая версия

Содержание

1 Введение
2 Оценка параметров смеси линейных моделей
- 2.1 Пример смеси линейных моделей
3 Оценка параметров смеси обобщенно-линейных моделей
- 3.1 Пример смеси логистических моделей
4 Оценка параметров смеси экспертов
5 Литература
6 Смотри также

Введение

В случае, когда одной модели для описания данных не хватает, используют смеси моделей. Предполагается, что исходная зависимость выражается формулой:

$p(\vec{y} | \vec{x}) = \sum_{k=1}^l p(\vec{w}_k | \vec{x}) p(y | \vec{x}, \vec{w}_k) = \sum_{k=1}^l \pi_k p(y | \vec{x}, \vec{w}_k),$

где $\pi_k = p(\vec{w}_k | \vec{x})$ --- вероятность принадлежности модели $k$ .

$\sum_{k=1}^l \pi_k = 1.$

Далее предполагается, что объекты в выборке независимы и плотность совместного распределения преобразуется в произведение плотностей распределения каждого объекта.

$p(\vec{y} | \vec{x}) = \sum_{k=1}^l \pi_k \prod_{i=1}^{n} p(y^i | \vec{x}^i, \vec{w}_k) = \prod_{i=1}^{n} \sum_{k=1}^l \pi_k p(y^i | \vec{x}^i, \vec{w}_k).$

Введем функцию правдоподобия $Q(\vec{w_1}, \dots, \vec{w_l}, \vec{\pi})$ как логарифм плотности вероятности данных.

$Q(\vec{w}^1, \dots, \vec{w}^l, \vec{\pi}) = \ln p(\vec{y} | \vec{x}) = \sum_{i=1}^{m} \ln \left[\sum_{k=1}^l \pi_k p(y^i | \vec{x}^i, \vec{w}_k)\right].$

Обозначим через $p(y, \vec{w}_k | \vec{x})$ вероятность того, что объект $(\vec{x}, y)$ был порожден компонентой $\vec{w}_k$ , $\gamma_{ik} = p(\vec{w}_k | y^i, \vec{x}^i)$ --- вероятность того, что $i$ -объект порожден $j$ -компонентой. Каждый объект был порожден какой-либо моделью, по формуле полной вероятности

$\sum_{k=1}^{l} \gamma_{ik} = 1, \quad \forall i.$

Для произвольного объекта $(\vec{x}, y)$ вероятность его получения моделью $w_k$ по формуле условной вероятности равна:

$p(y, \vec{w}_k | \vec{x}) = p(\vec{w}_k | \vec{x}) p(y | \vec{x}, \vec{w}_k) \equiv \pi_{k} p(y | \vec{x}, \vec{w}_k).$

Подставим это равенство в формулу Байеса для $\gamma_{ik}$

$\gamma_{ik} = \frac{\pi_k p(y^i | \vec{x}^i, \vec{w}_k)}{\sum_{s=1}^{l} \pi_s p(y^i | \vec{x}^i, \vec{w}_s)}.$

Для определения параметров смеси необходимо решить задачу максимизации правдоподобия $Q(\vec{w}^1, \dots, \vec{w}^l, \vec{\pi}) \rightarrow max$ , для этого выпишем функцию Лагранжа:

$L = \sum_{i=1}^{m} \ln \left[\sum_{k=1}^l \pi_k p(y^i | \vec{x}^i, \vec{w}^k)\right] - \lambda \left(\sum_{k=1}^{l} \pi_k - 1\right).$

Приравняем производные по $\pi_k$ и $\vec{w}_k$ функции Лагранжа к нулю получим, что:

$\pi_k = \frac{1}{m} \sum_{i=1}^{m} g_{ik}.$

и оптимизационная задача для нахождения параметров модели имеет вид:

$\sum_{i=1}^{m} \gamma_{ik} \ln p(y^i | \vec{x}^i, \vec{w}^k) \rightarrow \max_{\vec{w}^k}.$

В общем случае задача оптимизации $Q(\vec{w}^1, \dots, \vec{w}^l, \vec{\pi}) \rightarrow max$ трудна, для её решения используют EM алгоритм, заключающийся в итеративном повторении двух шагов. На $E$ -шаге вычисляются ожидаемые значения вектора скрытых переменных $\gamma_{ik}$ по текущему приближения параметров моделей $(\vec{w}_1, \dots, \vec{w}_l)$ . На $M$ -шаге решается задача максимизации правдоподобия $Q$ при начальном приближении параметров моделей и значений $\gamma_{ik}$ .

$E$ -шагу соответствует выражение

$\gamma_{ik} = \frac{\pi_k p(y^i | \vec{x}^i, \vec{w}_k)}{\sum_{s=1}^{l} \pi_s p(y^i | \vec{x}^i, \vec{w}_s)}.$

$M$ -шаг заключается в оптимизации параметров распределений.

$Q(\vec{w}^1, \dots, \vec{w}^l | \vec{\pi}) \rightarrow max$

Формула на $M$ -шаге может упроститься для случая конкретного распределения. Для упрощения дальнейших рассуждений введем обозначения

$G = (\vec{\gamma}_1, \dots, \vec{\gamma}_l) = \begin{pmatrix} \gamma_{11} & \dots & \gamma_{1l} \\ \vdots & \ddots & \vdots \\ \gamma_{m1} & \dots & \gamma_{ml} \\ \end{pmatrix}$ $G_k = \textrm{diag}(\vec{\gamma}_k).$

Оценка параметров смеси линейных моделей

Линейная модель имеет вид:

$\vec{y} = X\vec{w} + \vec{\eps},$

где $\vec{\eps} \sim \mathcal{N}(\vec{0}, B)$ --- вектор нормально распределенных ошибок. В данной постановке вектор $\vec{y}$ является нормальным с математическим ожиданием

$\mathsf{E}(y | \vec{x}) = \mu = \vec{x}^{T}\vec{w}$ , и корреляционной матрицей $B$ .

$p(\vec{y} | X, \vec{w}) = \frac{1}{(2\pi)^{\frac{n}{2}} \sqrt{|\textrm{det}B|}} \exp\left(-\frac{1}{2} (\vec{y} - X\vec{w})^{T} B (\vec{y} - X\vec{w}) \right).$

Шаг $M$ алгоритма примет следующий вид:

$G_k \ln\left[ \frac{1}{(2\pi)^{\frac{n}{2}} \sqrt{|\textrm{det}B|}}\right] -\frac{1}{2} \left(G_k (\vec{y} - X\vec{w})^{T} B (\vec{y} - X\vec{w}) \right) \rightarrow \max_{\vec{w}}$

Первое слагаемое не зависит от $\vec{w}_k$ , его можно не учитывать. Преобразование второго слагаемого дает

$\frac{1}{2} \vec{w}^{T} X^{T} G_k B X \vec{w} - \vec{w}^{T} X^{T} G_k B \vec{y} \rightarrow \min_{\vec{w}}$

Задача квадратична по $\vec{w}$ , решение находится аналитически

$\vec{w}^* = \left( X^{T} G_k B X \right)^{-1} G_k B X \vec{y}.$

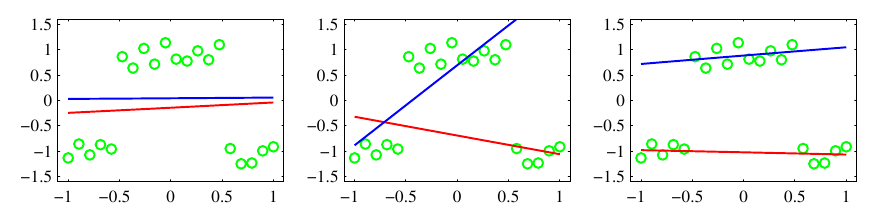
Пример смеси линейных моделей

Оценка параметров смеси обобщенно-линейных моделей

В случае обобщенных линейный моделей функция плотности распределения имеет вид

$p(\vec{y} | \vec{\theta}) = \exp \left( \vec{T}(\vec{y})^{T} \vec{\eta}(\vec{\theta}) - b(\vec{\theta}) + c(\vec{y}) \right).$

$M$ -шаг алгоритма сводится к максимизации

$G_k \vec{T}(\vec{y})^{T} \vec{\eta}(\vec{\theta}) - G_k b(\vec{\theta}) + G_k c(\vec{y}) \rightarrow \max_{\vec{\theta}}.$

Последнее слагаемое не зависит от параметров модели $\theta$ , что позволяет упростить функционал

$G_k \vec{T}(\vec{y})^{T} \vec{\eta}(\vec{\theta}) - G_k b(\vec{\theta}) \rightarrow \max_{\vec{\theta}}.$

Дальнейшая минимизация зависит от конкретного семейства из обобщенного класса, вида функции $b(\theta)$ .

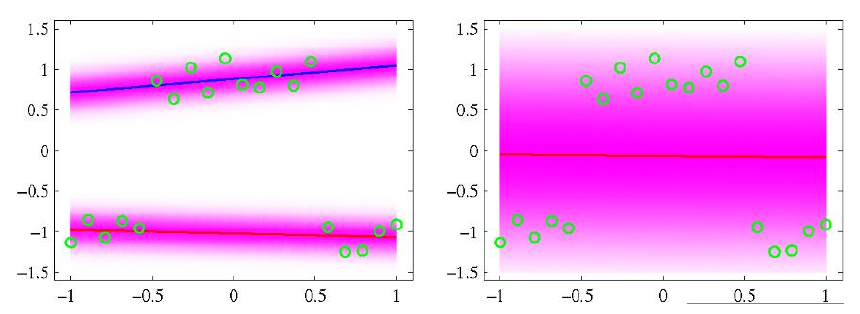
Пример смеси логистических моделей

На изображениях классификация одной и двумя моделями. Розовым показына плотность распределения зависимой переменной.

Оценка параметров смеси экспертов

Понятие смеси экспертов было введено Якобсом (Jacobs) в 1991г. Предполагается, что параметры смеси $\pi$ являются функциями от объекта, т.е.

$p(\vec{y} | \vec{x}) = \sum_{k=1}^l \pi_k(\vec{x}) p(y | \vec{x}, \vec{w}_k).$

Компоненты $\pi_k(\vec{x})$ называются функциями селективности, а $p(y | \vec{x}, \vec{w}_k)$ экспертами. Функция селективности отвечает за компетентность эксперта в определенной области.

Оказывается (Jordan and Jacobs, 1994), что наличие функции компетенции допускает решение задачи с помощью $EM$ -алгоритма, причем, $E$ -шаг остается прежним:

$\gamma_{ik} = \frac{\pi_k(\vec{x}^i) p(y^i | \vec{x}^i, \vec{w}_k)}{\sum_{s=1}^{l} \pi_s(\vec{x}^i) p(y^i | \vec{x}^i, \vec{w}_s)}.$

$M$ -шаг принимает вид:

$\pi_k = \frac{1}{m} \sum_{i=1}^{m} g_{ik}.$

$\sum_{i=1}^{m} \gamma_{ik}(\vec{x}^i) \ln p(y^i | \vec{x}^i, \vec{w}^k) \rightarrow \max_{\vec{w}^k}.$

Последенее уравнение можно решить с помощью метода итеративно перевзвешенных наименьших квадратов ( IRLS).

Литература

Смотри также

Данная статья была создана в рамках учебного задания.

Студент: Кирилл Павлов

Преподаватель: В.В. Стрижов

Срок: 26 сентября 2011

В настоящее время задание завершено и проверено. Данная страница может свободно правиться другими участниками проекта MachineLearning.ru.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9E%D1%86%D0%B5%D0%BD%D0%BA%D0%B0_%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%BE%D0%B2_%D1%81%D0%BC%D0%B5%D1%81%D0%B8_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B5%D0%B9»

Категория: Практика и вычислительные эксперименты

@@ Строка 94: / Строка 94: @@
 	G_k = \textrm{diag}(\vec{\gamma}_k).
 </tex>
-Пример смеси линейных моделей:
-[[Изображение:linear_convergence.png]]
 ==Оценка параметров смеси линейных моделей==
@@ Строка 133: / Строка 129: @@
 	\vec{w}^* = \left( X^{T} G_k B X \right)^{-1} G_k B X \vec{y}.
 </tex>
+====Пример смеси линейных моделей====
+[[Изображение:linear_convergence.png]]
 ==Оценка параметров смеси обобщенно-линейных моделей==
@@ Строка 154: / Строка 154: @@
 Дальнейшая минимизация зависит от конкретного семейства из обобщенного класса, вида функции <tex>b(\theta)</tex>.
+====Пример смеси логистических моделей====
+[[Изображение:logit_convergence.png]]
+На изображениях классификация одной и двумя моделями. Розовым показына плотность распределения зависимой переменной.
 ==Оценка параметров смеси экспертов==
@@ Строка 164: / Строка 170: @@
 Компоненты <tex> \pi_k(\vec{x})</tex>  называются функциями селективности, а <tex> p(y | \vec{x}, \vec{w}_k)</tex>  экспертами. Функция селективности отвечает за компетентность эксперта в определенной области.
+Оказывается (Jordan and Jacobs, 1994), что наличие функции компетенции допускает решение задачи с помощью <tex>EM</tex>-алгоритма, причем, <tex>E</tex>-шаг остается прежним:
+<tex>
+	\gamma_{ik} = \frac{\pi_k(\vec{x}^i) p(y^i | \vec{x}^i, \vec{w}_k)}{\sum_{s=1}^{l} \pi_s(\vec{x}^i) p(y^i | \vec{x}^i, \vec{w}_s)}.
+</tex>
+<tex>M</tex>-шаг принимает вид:
+<tex>
+	\pi_k = \frac{1}{m} \sum_{i=1}^{m} g_{ik}.
+</tex>
+<tex>
+	\sum_{i=1}^{m} \gamma_{ik}(\vec{x}^i) \ln p(y^i | \vec{x}^i, \vec{w}^k) \rightarrow \max_{\vec{w}^k}.
+</tex>
+Последенее уравнение можно решить с помощью метода итеративно перевзвешенных наименьших квадратов ([[Метод_наименьших_квадратов_с_итеративным_пересчётом_весов | IRLS]]).
 == Литература ==
@@ Строка 174: / Строка 198: @@
 * [[ЕМ-алгоритм, его модификации и обобщения]]
-{{Задание|Кирилл Павлов|В.В. Стрижов|26 сентября 2011|pavlov99|Strijov}}
+{{ЗаданиеВыполнено|Кирилл Павлов|В.В. Стрижов|26 сентября 2011|pavlov99|Strijov}}
 [[Категория:Практика и вычислительные эксперименты]]