Распределение Пуассона

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
м
м (→Свойства распределения Пуассона)
 
Строка 50: Строка 50:
: <tex>Y = \sum\limits_{i=1}^n Y_i \sim \mathrm{P}\left(\sum\limits_{i=1}^n \lambda_i\right).</tex>
: <tex>Y = \sum\limits_{i=1}^n Y_i \sim \mathrm{P}\left(\sum\limits_{i=1}^n \lambda_i\right).</tex>
-
* Пусть <tex>Y_i \sim \mathrm{P}(\lambda_i),\; i=1,2</tex>, и <tex>Y = Y_1 + Y_2.</tex> Тогда условное распределение <tex>Y_1</tex> при условии, что <tex>Y = y,</tex> биномиально. Более точно:
+
* Пусть <tex>Y_i \sim \mathrm{P}(\lambda_i),\; i=1,2,</tex> и <tex>Y = Y_1 + Y_2.</tex> Тогда условное распределение <tex>Y_1</tex> при условии, что <tex>Y = y,</tex> биномиально. Более точно:
: <tex>Y_1\mid Y = y \sim \mathrm{Bin}\left(y, \frac{\lambda_1}{\lambda_1+\lambda_2}\right). </tex>
: <tex>Y_1\mid Y = y \sim \mathrm{Bin}\left(y, \frac{\lambda_1}{\lambda_1+\lambda_2}\right). </tex>
[[Категория:Вероятностные распределения]]
[[Категория:Вероятностные распределения]]

Текущая версия

Распределение Пуассона
Функция вероятности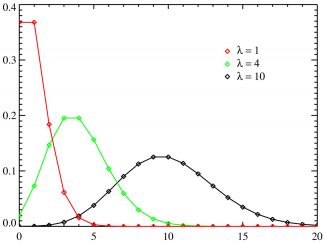
Plot of the Poisson PMF
Функция распределения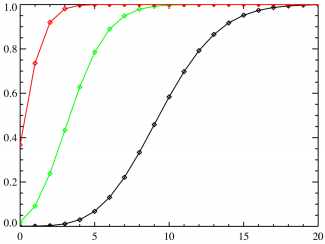
Plot of the Poisson CMF
Параметры \lambda \in (0,\infty)
Носитель k \in \{0,1,2,\ldots\}
Функция вероятности \frac{e^{-\lambda} \lambda^k}{k!}\!
Функция распределения \frac{\Gamma(k+1, \lambda)}{k!}\!
Математическое ожидание \lambda\,
Медиана N/A
Мода \lfloor\lambda\rfloor
Дисперсия \lambda\,
Коэффициент асимметрии \lambda^{-1/2}\,
Коэффициент эксцесса \lambda^{-1}\,
Информационная энтропия \lambda[1\!-\!\ln(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\ln(k!)}{k!}
Производящая функция моментов \exp(\lambda (e^t-1))\,
Характеристическая функция \exp(\lambda (e^{it}-1))\,

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение

Выберем фиксированное число \lambda > 0 и определим дискретное распределение, задаваемое следующей функцией вероятности:

p(k) \equiv \mathbb{P}(Y=k) = \frac{\lambda^k}{k!}\, e^{-\lambda},

где

  • k! обозначает факториал,
  • e = 2.718281828\ldots — основание натурального логарифма.

Тот факт, что случайная величина Y имеет распределение Пуассона с параметром \lambda, записывается: Y \sim~ \mathrm{P}(\lambda).

Моменты

Производящая функция моментов распределения Пуассона имеет вид:

E_Y(t)=e^{\lambda\left(e^t-1\right)},

откуда

\mathbb{M}[Y]=\lambda,
\mathbb{D}[Y]=\lambda.

Для факториальных моментов распределения справедлива общая формула:

\mathbb{M}Y^{[k]}=\lambda^k,

где k=1,2,...

А так как моменты и факториальные моменты линейным образом связаны, то часто для Пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.

Свойства распределения Пуассона

  • Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть Y_i\sim\mathrm{P}(\lambda_i),\; i=1,\ldots,n. Тогда
Y = \sum\limits_{i=1}^n Y_i \sim \mathrm{P}\left(\sum\limits_{i=1}^n \lambda_i\right).
  • Пусть Y_i \sim \mathrm{P}(\lambda_i),\; i=1,2, и Y = Y_1 + Y_2. Тогда условное распределение Y_1 при условии, что Y = y, биномиально. Более точно:
Y_1\mid Y = y \sim \mathrm{Bin}\left(y, \frac{\lambda_1}{\lambda_1+\lambda_2}\right).
Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%9F%D1%83%D0%B0%D1%81%D1%81%D0%BE%D0%BD%D0%B0»