Коррелограмма

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
(Новая: здесь будет статья про корелограмму)
Строка 1: Строка 1:
-
здесь будет статья про корелограмму
+
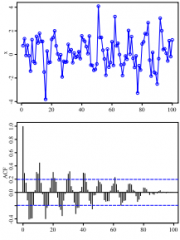
[[Image:Acf.png|thumb|right|На приведенных графиках представлена – вверху псевдохаотическая выборка из 100 элементов со скрытой синусоидальной зависимостью Внизу – график автокорреляции (Коррелограмма).]]
 +
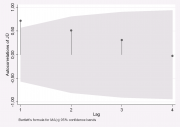
[[Image:Correlogram.png|thumb|Пример коррелограммы]]
 +
В анализе временных рядов коррелограмма, также известная как график автокорреляции, является графиком автокорреляций выборки <tex>r_h\,</tex> , от h (временная задержка).
 +
 
 +
Если используется кросс-корреляция , то ее называют кросс-коррелограммой. Коррелограмма - обычно используемый инструмент для того, чтобы проверить хаотичность в наборе данных. Эта хаотичность проверяется вычислением автокорреляций значений данных с переменными временными задержками. Если данные действительно случайны, такие автокорреляции должны быть близки к нулю для любого и каждого значения сдвига по времени. Если неслучайны (имеется скрытая осциллирующая зависимость), то одна или больше автокорреляций будут значительно отличаться от нуля. Кроме того, используются на стадии идентификации моделей в методе Box-Jenkins для авторегрессивных моделей временных рядов со скользящим средним значением. Значение коэффициентов автокорреляции должно быть почти равно нулю для хаотических процессов; если аналитик не проверяет выборку на хаотичность, то законность многих его статистических заключений ставится под подозрение. Коррелограммы - превосходный способ проверки хаотичности (или напротив – взаимосвязанности измерений).
 +
 
 +
==Вопросы==
 +
 
 +
Коррелограммы предназначены для того . чтобы обеспечить ответы на следующие вопросы:
 +
*Действительно ли данные случайны?
 +
*Yаблюдение связано со смежным наблюдением? наблюдение связано с вдвое удаленным наблюдением? (и т.д).
 +
*Имеет ли наблюдаемый временной ряд белый шум?
 +
*Действительно ли наблюдаемый временной ряд является синусоидальным?
 +
*Действительно ли наблюдаемыйвременной ряд авторегрессивен?
 +
*Какова соответствующая модель для наблюдаемого временного ряда?
 +
*Является ли модель <tex>Y = \mathrm{constant} + \mathrm{error }</tex> надежной и достаточной?
 +
*Является ли формула <tex>s_{\bar{Y}}=s/\sqrt{N}</tex> правильной?
 +
 
 +
==Важность==
 +
 
 +
Хаотичность (наряду с неподвижной моделью, установленным изменением, и установленным распределением) является одним из четырех предположений, которые типично лежат в основе всех процессов измерения.
 +
Предположение хаотичности критически важно по следующим трем причинам:
 +
1.Большинство стандартных статистических тестов зависит от хаотичности. Законность испытательных заключений непосредственно связана с законностью предположения хаотичности.
 +
2.Многие обычно используемые статистические формулы зависят от предположения хаотичности. Самая общая формула стандартного отклонения серии измерений есть
 +
<tex>s_{\bar{Y}}=s/\sqrt{N}</tex>
 +
где s - стандартное отклонение единичного измерения данных. Хотя следствия из этой формулы повсеместно используются, проведенный анализ не будет представлять никакой ценности, если предположение о хаотичности не доказано.
 +
3.Для одномерных данных модель «по умолчанию» - <tex>Y = \mathrm{constant} + \mathrm{error }</tex>. Если данные не случайны, эта модель является неправильной и недействительной, и оценки для параметров (таких как константа) тоже становятся бессмысленными и недействительными.
 +
 
 +
==Оценка автокорреляций==
 +
Коэффициент автокорреляции для временной задержки h дается формулой:
 +
:<tex>r_h = c_h/c_0</tex>
 +
где ''c<sub>h</sub>'' - функция автоковариации
 +
:<tex>c_h = \frac{1}{N}\sum_{t=1}^{N-h} \left(Y_t - \bar{Y}\right)\left(Y_{t+h} - \bar{Y}\right)</tex>
 +
и ''c<sub>0</sub>'' – функция вариации
 +
:<tex>c_0 = \frac{1}{N}\sum_{t=1}^{N} \left(Y_t - \bar{Y}\right)^2</tex>
 +
Примечания:
 +
*Коэффициент автокорреляции ''r<sub>h</sub>'' всегда находится между -1 и +1.
 +
*Некоторые источники могут использовать следующую формулу для функции автоковариации:
 +
:<tex>c_h = \frac{1}{N-h}\sum_{t=1}^{N-h} \left(Y_t - \bar{Y}\right)\left(Y_{t+h} - \bar{Y}\right)</tex>
 +
 +
Хотя в формуле этого определения вычисляется меньший наклон (или как еще говорят - покатость), (1/N) формулировка имеет некоторые желательные статистические свойства и является формой, обычно используемой в статистической литературе.
 +
 
 +
==Статистический вывод коррелограмм==
 +
На одном и том же графике можно «покачать» верхнюю и нижнюю границы автокорреляции с помощью параметра уровня значимости <tex>\alpha\,</tx>:
 +
 
 +
:<tex>B=\pm z_{1-\alpha/2} SE(r_h)</tex> где <tex>r_h\,</tex> есть оценка автокорреляции для временного лага <tex>h\,</tex>.
 +
 
 +
Если автокорреляция оказывается выше (ниже) чем это верхнее (нижнее) граничное значение, нуль-гипотеза, что якобы нет никакой автокорреляции для данной временной задержки и вне ее, такая гипотеза должна быть отклонена на уровне значимости <tex>\alpha\,</tex>.
 +
 
 +
Этот тест - приблизительный и предполагает, что временной ряд является Гауссовским. В вышеупомянутом случае z<sub>1-α/2</sub> - квантиль нормального распределения; SE - стандартная ошибка, которая может быть вычислена по формуле Bartlett’а:
 +
 
 +
:<tex>SE(r_1)=\frac {1} {N} </tex>
 +
:<tex> SE(r_h)=\sqrt\frac{1+2\sum_{i=1}^{h-1} r^2_i}{N}</tex> for <tex>h>1\,</tex>
 +
 
 +
На вышеприведенных графиках мы можем отклонить нуль-гипотезу, что нет никакой автокорреляции между соседними по времени точками (для смежных точек lag=1). В течение других периодов нельзя отклонить нуль-гипотезу об отсутствии автокорреляции.
 +
 
 +
Отметим, что есть две отличных формулы для вычисления доверительных интервалов:
 +
1.Если коррелограмма используется для проверки на хаотичность (то есть, нет никакой временной зависимости в данных), рекомендуется следующая формула:
 +
 
 +
:<tex>\pm \frac{z_{1-\alpha/2}}{\sqrt{N}} </tex>
 +
 
 +
где N – размер выборки, z - функция квантиля стандартного нормального распределения, и α - уровень значимости. В этом случае, доверительный интервал имеет фиксированную ширину, которая зависит от размера выборки.
 +
 
 +
2.Коррелограммы также используются на стадии идентификации моделей при подгонке с использованием метода скользящего среднего (например, модель ARIMA). В этом случае доверительный интервал увеличивается по мере увеличения задержки (лага) k:
 +
 
 +
:<tex>\pm z_{1-\alpha/2}\sqrt{\frac{1}{N}\left(1+2\sum_{i=1}^{k} y_i^2\right)}</tex>
 +
 
 +
==Внешние ссылки==
 +
*[http://www.itl.nist.gov/div898/handbook/eda/section3/eda331.htm Автокорреляционный график]
 +
 
 +
==Литература==
 +
* Hanke, John E./Reitsch, Arthur G./Wichern, Dean W. (2001). Business forecasting (7th edition ed.). Prentice Hall.
 +
* Box, G. E. P., and Jenkins, G. (1976). Time Series Analysis: Forecasting and Control. Holden-Day.
 +
* Chatfield, C. (1989). The Analysis of Time Series: An Introduction (Fourth Edition ed.). Chapman & Hall.

Версия 06:28, 10 января 2009

На приведенных графиках представлена – вверху псевдохаотическая выборка из 100 элементов со скрытой синусоидальной зависимостью Внизу – график автокорреляции (Коррелограмма).
На приведенных графиках представлена – вверху псевдохаотическая выборка из 100 элементов со скрытой синусоидальной зависимостью Внизу – график автокорреляции (Коррелограмма).
Пример коррелограммы
Пример коррелограммы

В анализе временных рядов коррелограмма, также известная как график автокорреляции, является графиком автокорреляций выборки r_h\, , от h (временная задержка).

Если используется кросс-корреляция , то ее называют кросс-коррелограммой. Коррелограмма - обычно используемый инструмент для того, чтобы проверить хаотичность в наборе данных. Эта хаотичность проверяется вычислением автокорреляций значений данных с переменными временными задержками. Если данные действительно случайны, такие автокорреляции должны быть близки к нулю для любого и каждого значения сдвига по времени. Если неслучайны (имеется скрытая осциллирующая зависимость), то одна или больше автокорреляций будут значительно отличаться от нуля. Кроме того, используются на стадии идентификации моделей в методе Box-Jenkins для авторегрессивных моделей временных рядов со скользящим средним значением. Значение коэффициентов автокорреляции должно быть почти равно нулю для хаотических процессов; если аналитик не проверяет выборку на хаотичность, то законность многих его статистических заключений ставится под подозрение. Коррелограммы - превосходный способ проверки хаотичности (или напротив – взаимосвязанности измерений).

Содержание

Вопросы

Коррелограммы предназначены для того . чтобы обеспечить ответы на следующие вопросы:

  • Действительно ли данные случайны?
  • Yаблюдение связано со смежным наблюдением? наблюдение связано с вдвое удаленным наблюдением? (и т.д).
  • Имеет ли наблюдаемый временной ряд белый шум?
  • Действительно ли наблюдаемый временной ряд является синусоидальным?
  • Действительно ли наблюдаемыйвременной ряд авторегрессивен?
  • Какова соответствующая модель для наблюдаемого временного ряда?
  • Является ли модель Y = \mathrm{constant} + \mathrm{error } надежной и достаточной?
  • Является ли формула s_{\bar{Y}}=s/\sqrt{N} правильной?

Важность

Хаотичность (наряду с неподвижной моделью, установленным изменением, и установленным распределением) является одним из четырех предположений, которые типично лежат в основе всех процессов измерения. Предположение хаотичности критически важно по следующим трем причинам: 1.Большинство стандартных статистических тестов зависит от хаотичности. Законность испытательных заключений непосредственно связана с законностью предположения хаотичности. 2.Многие обычно используемые статистические формулы зависят от предположения хаотичности. Самая общая формула стандартного отклонения серии измерений есть s_{\bar{Y}}=s/\sqrt{N} где s - стандартное отклонение единичного измерения данных. Хотя следствия из этой формулы повсеместно используются, проведенный анализ не будет представлять никакой ценности, если предположение о хаотичности не доказано. 3.Для одномерных данных модель «по умолчанию» - Y = \mathrm{constant} + \mathrm{error }. Если данные не случайны, эта модель является неправильной и недействительной, и оценки для параметров (таких как константа) тоже становятся бессмысленными и недействительными.

Оценка автокорреляций

Коэффициент автокорреляции для временной задержки h дается формулой:

r_h = c_h/c_0

где ch - функция автоковариации

c_h = \frac{1}{N}\sum_{t=1}^{N-h} \left(Y_t - \bar{Y}\right)\left(Y_{t+h} - \bar{Y}\right)

и c0 – функция вариации

c_0 = \frac{1}{N}\sum_{t=1}^{N} \left(Y_t - \bar{Y}\right)^2

Примечания:

  • Коэффициент автокорреляции rh всегда находится между -1 и +1.
  • Некоторые источники могут использовать следующую формулу для функции автоковариации:
c_h = \frac{1}{N-h}\sum_{t=1}^{N-h} \left(Y_t - \bar{Y}\right)\left(Y_{t+h} - \bar{Y}\right)

Хотя в формуле этого определения вычисляется меньший наклон (или как еще говорят - покатость), (1/N) формулировка имеет некоторые желательные статистические свойства и является формой, обычно используемой в статистической литературе.

Статистический вывод коррелограмм

На одном и том же графике можно «покачать» верхнюю и нижнюю границы автокорреляции с помощью параметра уровня значимости \alpha\,</tx>: </dd></dl> <dl><dd><tex>B=\pm z_{1-\alpha/2} SE(r_h) где r_h\, есть оценка автокорреляции для временного лага h\,.

Если автокорреляция оказывается выше (ниже) чем это верхнее (нижнее) граничное значение, нуль-гипотеза, что якобы нет никакой автокорреляции для данной временной задержки и вне ее, такая гипотеза должна быть отклонена на уровне значимости \alpha\,.

Этот тест - приблизительный и предполагает, что временной ряд является Гауссовским. В вышеупомянутом случае z1-α/2 - квантиль нормального распределения; SE - стандартная ошибка, которая может быть вычислена по формуле Bartlett’а:

SE(r_1)=\frac {1} {N}
SE(r_h)=\sqrt\frac{1+2\sum_{i=1}^{h-1} r^2_i}{N} for h>1\,

На вышеприведенных графиках мы можем отклонить нуль-гипотезу, что нет никакой автокорреляции между соседними по времени точками (для смежных точек lag=1). В течение других периодов нельзя отклонить нуль-гипотезу об отсутствии автокорреляции.

Отметим, что есть две отличных формулы для вычисления доверительных интервалов: 1.Если коррелограмма используется для проверки на хаотичность (то есть, нет никакой временной зависимости в данных), рекомендуется следующая формула:

\pm \frac{z_{1-\alpha/2}}{\sqrt{N}}

где N – размер выборки, z - функция квантиля стандартного нормального распределения, и α - уровень значимости. В этом случае, доверительный интервал имеет фиксированную ширину, которая зависит от размера выборки.

2.Коррелограммы также используются на стадии идентификации моделей при подгонке с использованием метода скользящего среднего (например, модель ARIMA). В этом случае доверительный интервал увеличивается по мере увеличения задержки (лага) k:

\pm z_{1-\alpha/2}\sqrt{\frac{1}{N}\left(1+2\sum_{i=1}^{k} y_i^2\right)}

Внешние ссылки

Литература

   * Hanke, John E./Reitsch, Arthur G./Wichern, Dean W. (2001). Business forecasting (7th edition ed.). Prentice Hall. 
   * Box, G. E. P., and Jenkins, G. (1976). Time Series Analysis: Forecasting and Control. Holden-Day. 
   * Chatfield, C. (1989). The Analysis of Time Series: An Introduction (Fourth Edition ed.). Chapman & Hall.
Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9A%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0»
Личные инструменты