Участник:Айнагуль Джумабекова

Материал из MachineLearning.

(Различия между версиями)

Перейти к: навигация, поиск

Версия 13:12, 26 декабря 2008

Метод штрафных функций

Основная задача метода штрафных функций состоит в преобразовании задачи минимизации функции

$z=f(x)$

с соответствующими ограничениями, наложенными на х, в задачу поиска минимума без ограничений функции

$Z=f(x)+P(x)$

Функция $P(x)$ является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию Z, т.е. увеличивала её значение.В этом случае минимум функции Z будет находиться внутри области ограничений. Функция $P(x)$ , удовлетворяющая этому условию, может быть не единственной. Задачу минимизации можно сформулировать следующим образом:

минимизировать функцию $z=f(x)$

при ограничениях $c_j(x)>0,j=1,2,\dots,m$ .

Функцию $P(x)$ удобно записать следующим образом:

$P(x)=r\sum_{j=1}^m\frac{1}{c_j(x)}$

где r – положительная величина.

Тогда функция $Z=\varphi(x,r)$ принимает вид

$Z=\varphi(x,r)=f(x)+ r\sum_{j=1}^m\frac{1}{c_j(x)}$ .

Если х принимает допустимые значения, т.е. значения, для которых $c_j>=0$ , то Z принимает значения, которые больше соответствующих значений $f(x)$ (истинной целевой функции данной задачи), и разность можно уменьшить за счет того, что r может быть очень малой величиной. Но если х принимает значения, которые хотя и являются допустимыми, но близки к границе области ограничений, и по крайней мере одна из функций $c_j(x)$ близка к нулю, тогда значения функции $P(x)$ , и следовательно значения функции Z станут очень велики. Таким образом, влияние функции $P(x)$ состоит в создании «гребня с крутыми краями» вдоль каждой границы области ограничений. Следовательно, если поиск начнется из допустимой точки и осуществляется поиск минимума функции $\varphi(x,r)$ без ограничений, то минимум, конечно, будет достигаться внутри допустимой области для задачи с ограничениями. Полагая r достаточно малой величиной, для того чтобы влияние $P(x)$ было малым в точке минимума, мы можем сделать точку минимума функции $\varphi(x,r)$ без ограничений совпадающей с точкой минимума задачи с ограничениями.

Алгоритм метода штрафных функций

Пусть имеется следующая задача: Минимизировать $f(x)$ при ограничениях $g_i(x)\ge0$ , $i=\bar{1,m}$ .

Начальный этап Выбрать $\epsilon>0$ в качестве константы остановки, начальную допустимую точку $x^0 R^n$ , для которой $g_i(x^0)>0$ , $i=\bar{1,m}$ , скаляр $r_0$ и $0<\betta<1$ . Положить k=1 и перейти к основному этапу.

Основной этап. k-я итерация.

Первый шаг. При исходной точке $x_k$ решить следующую задачу безусловной оптимизации:

$P(x,r)=f(x)+\sum_{i=1}^mR_i(g_i(x))\omega_i$ минимизировать, где

$r>0$ - параметр, значения которого убывают с каждой итерации $R_i(t) \to \infty$ при $t \to 0$ ; $\omega_i$ - положительные весовые коэффициенты.

Примерами штрафных функций являются:

1) обратная функция $R_i(g_i(x))=\frac{1}{g_i(x)}$

2) логарифмическая функция $R_i(g_i(x))=-ln(g_i(x))$

Положить $x_{k+1}$ равным оптимальному решению задачи минимизации и перейти ко второму шагу.

Минимизация штрафной функцию может быть выполнена любым методом безусловной оптимизации, например, градиентным.

Второй шаг

Если $r_k\sumR(g_i(x_{k+1}))\omega_i<\epsilon$ , то остановиться. Решение является искомым. В противном случае положить $r_{k+1}=\bettar_k$ . Изменить $k=k+1$ и перейти к первому шагу (k+1)-й итерации.

Метод штрафных функций относится к группе методов внутренней точки, т.е. он начинает работать с допустимой точки $x_0$ и генерирует последовательность допустимых точек $x_1,x_2,\dots,x_n$ . Метод барьерных функций, наоборот, относится к группе методов внешней точки, он начинает поиск с недопустимой точки и генерирует последовательность недопустимых решений, которая приближается к оптимальному решению извне допустимой области.

Пусть имеется задача минимизировать $f(x)$ при ограничениях

::, 
:: ,

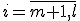
В частности, для искомых функций – ограничений целесообразно использовать барьерную функцию следующего вида:

$\alpha(x)=\sum_{i=1}^{m}R_1(g_i(x))+ \sum_{i=1}^{m}R_2(h_i(x))$

$R_1,R_2$ - непрерывные функции, которые удовлетворяют условиям: $R_1(y)=0$ , если $y>=0$ и $R_1(y)>0$ , если $y<0$ , $R_2(y)=0$ , если $y=0$ и $R_2(y)>0$ , если $y\not=0$ .

Типичными являются следующие выражения для функций $R_1,R_2$ : $R_1(y)=(max{0,-y})^p$ , $R_2(y)=|y|^p$ , где р – целое положительное число. Далее от исходной задачи переходим к задачи безусловной оптимизации вспомогательной функции: минимизировать $f(x)+r\alpha(x)$ , где $r>0$ - штрафной коэффициент. Пусть – непрерывная функция. Обозначим $\tetta(r)=inf{f(x)+r\alpha(x)}$ .

Подход, связанный с барьерной ф

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%A3%D1%87%D0%B0%D1%81%D1%82%D0%BD%D0%B8%D0%BA:%D0%90%D0%B9%D0%BD%D0%B0%D0%B3%D1%83%D0%BB%D1%8C_%D0%94%D0%B6%D1%83%D0%BC%D0%B0%D0%B1%D0%B5%D0%BA%D0%BE%D0%B2%D0%B0»

@@ Строка 5: / Строка 5: @@
 ::<tex>Z=f(x)+P(x)</tex>
-Функция <tex>P(x)</tex> является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию Z будет находиться внутри области ограничений. Функция <tex>P(x)</tex>, удовлетворяющая этому условию, может быть не единственной.
+Функция <tex>P(x)</tex> является штрафной. Необходимо, чтобы при нарушении ограничений она «штрафовала» функцию Z, т.е. увеличивала её значение.В этом случае минимум функции Z  будет находиться внутри области ограничений. Функция <tex>P(x)</tex>, удовлетворяющая этому условию, может быть не единственной.
 Задачу минимизации можно сформулировать следующим образом:
-минимизировать функцию  <tex>z=f(x)</tex>
+::минимизировать функцию  <tex>z=f(x)</tex>
 при ограничениях <tex>c_j(x)>0,j=1,2,\dots,m</tex>.
@@ Строка 24: / Строка 24: @@
 Пусть имеется следующая задача:
-Минимизировать <tex>f(x)</tex> при ограничениях <tex>g_i(x)>=0</tex>,<tex>i=\bar{1,m}</tex>.
+Минимизировать <tex>f(x)</tex> при ограничениях <tex>g_i(x)\ge0</tex>,<tex>i=\bar{1,m}</tex>.
 '''Начальный этап''' Выбрать <tex>\epsilon>0</tex> в качестве константы остановки, начальную допустимую точку <tex>x^0 R^n</tex>, для которой <tex>g_i(x^0)>0</tex>, <tex>i=\bar{1,m}</tex>, скаляр <tex>r_0</tex> и <tex>0<\betta<1</tex>. Положить k=1 и перейти к основному этапу.
@@ Строка 61: / Строка 61: @@
 <tex>R_1,R_2</tex> - непрерывные функции, которые удовлетворяют условиям:
 <tex>R_1(y)=0</tex> , если <tex>y>=0</tex> и <tex>R_1(y)>0</tex> , если <tex>y<0</tex>,
-<tex>R_2(y)=0</tex> , если <tex>y=0</tex>   и <tex>R_2(y)>0</tex> , если <tex>y!=0</tex>.
+<tex>R_2(y)=0</tex> , если <tex>y=0</tex>   и <tex>R_2(y)>0</tex> , если <tex>y\not=0</tex>.
 Типичными являются следующие выражения для функций <tex>R_1,R_2</tex>:

Участник:Айнагуль Джумабекова

Материал из MachineLearning.

Версия 13:12, 26 декабря 2008

Метод штрафных функций

Алгоритм метода штрафных функций

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты