Критерий хи-квадрат

Материал из MachineLearning.

(Различия между версиями)

Версия 19:39, 8 декабря 2008

Содержание

1 Определение
2 Проверка гипотезы
3 Пример
4 Сложная гипотеза
5 Литература
6 Ссылки

Определение

Критерий $\chi^2$ - наиболее часто используемый статистический критерий для проверки гипотезы $H_0$ , что наблюдаемая случайная величина подчиняется некому теоретическому закону распределения.

Пусть дана случайная величина X .

Гипотеза $H_0$ : с. в. X подчиняется закону распределения $F(x)$ .

Для проверки гипотезы рассмотрим выборку, состоящую из n независимых наблюдений над с.в. X: $X^n = \left( x_1, \cdots \x_n \right), \; x_i \in \left[ a, b \right], \; \forall i=1 \dots n$ . По выборке построим эмпирическое распределение $F^*(x)$ с.в X. Сравнение эмпирического $F^*(x)$ и теоретического распределения $F(x)$ производится с помощью специально подобранной случайной величины — критерия согласия. Рассмотрим критерий согласия Пирсона (критерий $\chi^2$ ):

Гипотеза $H_0^*$ : Хⁿ порождается функцией $F^*(x)$ .

Разделим [a,b] на k непересекающихся интервалов $(a_i, b_i], \; i=1 \dots k$ ;

Пусть $n_j$ - количество наблюдений в j-м интервале: $n_j = \sum_{i=1}^n \left[ a_i <x \leq b_i \right]$ ;

$p_j = F(b_j)-F(a_j)$ - вероятность попадания наблюдения в j-ый интервал при выполнении гипотезы $H_0^*$ ;

$E_j = np_j$ Ожидаемое число попаданий в j-ый интервал;

Статистика: $\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-1}^2$ - Распределение хи-квадрат с k-1 степенью свободы.

Проверка гипотезы 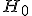$H_0$

Распределение хи-квадрат

В зависимости от значения критерия $\chi^2$ , гипотеза $H_0$ может приниматься, либо отвергаться:

$\chi^2_1 < \chi^2 < \chi^2_2$ , гипотеза $H_0$ выполняется.

$\chi^2 \leq \chi^2_1$ (попадает в левый "хвост" распределения) гипотеза $H_0$ отвергается.

$\chi^2 \geq \chi^2_2$ (попадает в правый "хвост" распределения) гипотеза $H_0$ отвергается.

Пример

Проверим гипотезу $H_0$ : если взять случайную выборку 100 человек из некоторой популяции, в которой количество мужчин и женщин примерно одинаково (встречаются с одинаковой частотой), то в наблюдаемой выборке отношение количества мужчин и женщин будет соотноситься с частотой по всей популяции (50/50). Пусть в наблюдаемой выборке 46 мужчин и 54 женщины, тогда число степеней свобод $k-1=2-1=1$ и

$\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j}= \frac{\left(46-50 \right)^2}{50}+\frac{\left(54-50 \right)^2}{50}=0,64$

Т.о. при уровне значимости $\alpha=0.05$ гипотеза $H_0$ выполняется (см таблицу значений ф-ии $\chi^2_k$ ).

Сложная гипотеза

Гипотеза $H_0^*$ : Хⁿ порождается функцией $F(x,\theta),\; \theta \in R^d,\; \theta$ - неизвестна. Найдем $\hat{\theta}$ с помощью метода максимального правдоподобия.

$p_j(\theta)=F(b_j,\theta)-F(a_j,\theta)$ , $n_j = \sum_{i=1}^n \left[ a_i <x \leq b_i \right]$ , $\left(a_j,b_j \right]$ - фиксированы при $j=1 \dots k$ .

$\hat{\theta} = \arg \max_{\theta} \sum n_j \ln p_j(\theta)$

Теорема Фишера $\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-d-1}^2$ , где $E_j=n p_j\left(\hat{\theta}\right)$

Литература

Ссылки

[Критерий хи-квадрат (en.wiki)]

Это незавершённая статья. Вы поможете проекту, исправив и дополнив её.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%9A%D1%80%D0%B8%D1%82%D0%B5%D1%80%D0%B8%D0%B9_%D1%85%D0%B8-%D0%BA%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82»

Категории: Незавершённые статьи | Прикладная статистика | Энциклопедия анализа данных

@@ Строка 1: / Строка 1: @@
 {{TOCright}}
-{{UnderConstruction|[[Участник:Венжега Андрей|Венжега Андрей]] 00:08, 14 ноября 2008 (MSK)}}
 == Определение ==
@@ Строка 25: / Строка 24: @@
 <tex>E_j = np_j</tex> Ожидаемое число попаданий в j-ый интервал;
-'''Статистика:''' <tex>\chi^2 = \sum_{i=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-1}^2</tex>  - [[Распределение хи-квадрат|Распределение хи-квадрат]] с k-1 степенью свободы.
+'''Статистика:''' <tex>\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-1}^2</tex>  - [[Распределение хи-квадрат|Распределение хи-квадрат]] с k-1 степенью свободы.
 == Проверка гипотезы <tex>H_0</tex> ==
@@ Строка 36: / Строка 35: @@
 * <tex>\chi^2 \geq \chi^2_2</tex> (попадает в правый "хвост" распределения) гипотеза <tex>H_0</tex> отвергается.
+== Пример ==
+Проверим гипотезу <tex>H_0</tex>: если взять случайную выборку 100 человек из некоторой популяции, в которой количество мужчин и женщин примерно одинаково (встречаются с одинаковой частотой), то в наблюдаемой выборке отношение количества мужчин и женщин будет соотноситься с частотой по всей популяции (50/50). Пусть в наблюдаемой выборке 46 мужчин и 54 женщины, тогда число степеней свобод <tex>k-1=2-1=1</tex> и
+<tex>\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j}= \frac{\left(46-50 \right)^2}{50}+\frac{\left(54-50 \right)^2}{50}=0,64 </tex>
+Т.о. при уровне значимости <tex>\alpha=0.05</tex> гипотеза <tex>H_0</tex> выполняется (см таблицу значений ф-ии <tex>\chi^2_k</tex>).
 == Сложная гипотеза ==
-== Теорема Фишера ==
+Гипотеза <tex>H_0^*</tex>: Х<sup>n</sup> порождается функцией <tex>F(x,\theta),\; \theta \in R^d,\;  \theta</tex> - неизвестна. Найдем <tex>\hat{\theta}</tex> с помощью [[Метод максимального правдоподобия|метода максимального правдоподобия]].
+<tex>p_j(\theta)=F(b_j,\theta)-F(a_j,\theta)</tex>, <tex> n_j = \sum_{i=1}^n \left[ a_i <x \leq b_i \right] </tex>, <tex>\left(a_j,b_j \right]</tex> - фиксированы при <tex>j=1 \dots k</tex>.
+<tex>\hat{\theta} = \arg \max_{\theta} \sum n_j \ln p_j(\theta) </tex>
+'''Теорема Фишера''' <tex>\chi^2 = \sum_{j=1}^k \frac{ \left( n_j-E_j \right)^2}{E_j} \sim \chi_{k-d-1}^2</tex>, где  <tex>E_j=n p_j\left(\hat{\theta}\right)</tex>
 == Литература ==

Критерий хи-квадрат

Материал из MachineLearning.

Версия 19:39, 8 декабря 2008

Содержание

Определение

Проверка гипотезы $H_0$

Пример

Сложная гипотеза

Литература

Ссылки

Просмотры

Личные инструменты

Навигация

Поиск

Инструменты