Материал из MachineLearning.
(Различия между версиями)
|
|
| Строка 3: |
Строка 3: |
| | === Постановка математической задачи === | | === Постановка математической задачи === |
| | | | |
| - | Одной из основных задач численного анализа является задача об интерполяции функций. | + | Одной из значения функции <tex>y(x)</tex>, равные <tex>y(x_0)=y_0,\cdots,y(x_i)=y_i,\cdots,y(x_n)=y_n</tex>. Требуется построить ''иносновных задач численного анализа является задача об интерполяции функций. |
| - | Пусть на отрезке <tex>a\le \x\le \b</tex> задана сетка <tex>\omega=\{x_i:x_0=a<x_1<\cdots<x_i<\cdots<x_n=b\}</tex> и в её узлах заданы значения функции <tex>y(x)</tex>, равные <tex>y(x_0)=y_0,\cdots,y(x_i)=y_i,\cdots,y(x_n)=y_n</tex>. Требуется построить ''интерполянту'' — функцию <tex>f(x)</tex>, совпадающую с функцией <tex>y(x)</tex> в узлах сетки: | + | Пусть на отрезке <tex>a\le \x\le \b</tex> задана сетка <tex>\omega=\{x_i:x_0=a<x_1<\cdots<x_i<\cdots<x_n=b\}</tex> и в её узлах заданы |
| | + | терполянту'' — функцию <tex>f(x)</tex>, совпадающую с функцией <tex>y(x)</tex> в узлах сетки: |
| | {{ eqno | 1 }} | | {{ eqno | 1 }} |
| | <p align="center"><tex>f(x_i)=y_i, i=0,1,\cdots,n.</tex></p> | | <p align="center"><tex>f(x_i)=y_i, i=0,1,\cdots,n.</tex></p> |
| Строка 113: |
Строка 114: |
| | | | |
| | == Числовой пример == | | == Числовой пример == |
| - | Вычислим по формулам прямоугольников и трапеций при <tex>n=2</tex> интеграл
| + | Построим интерполянту для для функции <tex>ftex> заданой следующим образом: |
| - | | + | {| class="wikitable" |
| - | {{ eqno | 14 }}
| + | |- |
| - | <p align="center"><tex>I=\int_{0}^{\pi/2}{\sin(x)dx} = 1</tex></p>
| + | ! <tex>xtex> |
| - | | + | ! <tex>f(x)</tex> |
| - | В данном случае
| + | |- |
| - | | + | | 1 |
| - | | + | | 1.0002 |
| - | <p align="center"><tex>P_2=\frac{\pi}{4}(\sin(\frac{\pi}{8})+\sin(\frac{3\pi}{8}))=1.026172</tex></p>
| + | |- |
| - | | + | | 2 |
| - | <p align="center"><tex>T_2=\frac{\pi}{4}(\frac{1}{2}\sin(0)+\sin(\frac{\pi}{4})+\frac{1}{2}\sin(\frac{\pi}{2}))=0.948059</tex></p>
| + | | 1.0341 |
| - | | + | |- |
| - | Зная точный ответ (14), найдем погрешности
| + | | 3 |
| - | | + | | 0.6 |
| - | {{ eqno | 15 }}
| + | |- |
| - | <p align="center"><tex>\alpha_2=-0.026172,\beta_2=0.051941</tex></p>
| + | | 4 |
| - | | + | | 0.40105 |
| - | Вторая производная функции <tex>\sin(x)</tex> на отрезке <tex>[0,\pi/2]</tex> отрицательна, ее модуль не превышает единицы: <tex>M_2=1</tex>. Величина погрешностей (15) удовлетворяет неравенствам (9) и (13):
| + | |- |
| - | | + | | 5 |
| - | <p align="center"><tex>|\alpha_2|\le \frac{1}{96}(\frac{\pi}{2})^3<0.041,|\beta_2|\le \frac{1}{48}(\frac{\pi}{2})^3<0.081</tex></p>
| + | | 0.1 |
| - | | + | |- |
| | + | | 6 |
| | + | | 0.23975 |
| | + | |} |
| | + | [[Изображение:graph1.png|thumb]] |
| | == Рекомендации программисту == | | == Рекомендации программисту == |
| | | | |
| - | === Автоматический выбор шага интегрирования ===
| |
| - |
| |
| - | Величина погрешности численного интегрирования зависит как от шага сетки <tex>h</tex>, так и от гладкости подынтегральной функции <tex>f(x)</tex>. Например, в оценку (11), наряду с <tex>h</tex>, входит величина
| |
| - |
| |
| - | <p align="center"><tex>M_{2,i}=\underset{x\in [x_{i-1},x_i]}{max}|f''(x)|,</tex></p>
| |
| - |
| |
| - | которая может сильно меняться от точки к точке и, вообще говоря, заранее неизвестна. Если величина погрешности велика, то ее можно уменьшить путем измельчения сетки на данном отрезке <tex>[x_{i-1},x_i]</tex>. Для этого прежде всего надо уметь апостериорно, т.е. после проведения расчета, оценивать погрешность.
| |
| - |
| |
| - | Апостериорную оценку погрешности можно осуществить ''методом Рунге''. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности <tex>m</tex>, т.е. <tex>I_i-I_{h,i}\approx c_i h_i^m</tex>. Тогда
| |
| - |
| |
| - | <p align="center"><tex>I_i-I_{h/2,i}\approx c_i (\frac{h_i}{2})^m,</tex></p>
| |
| - |
| |
| - | откуда получим
| |
| - |
| |
| - | {{ eqno | 16 }}
| |
| - | <p align="center"><tex>I_i-I_{h,i}\approx 2^m (I_i-I_{h/2,i}),</tex></p>
| |
| - |
| |
| - | {{ eqno | 17 }}
| |
| - | <p align="center"><tex>I_i-I_{h/2,i}\approx \frac{I_{h/2,i}-I_{h,i}}{2^m-1}</tex></p>
| |
| - |
| |
| - | Возможность апостериорно оценивать погрешность позволяет вычислять интеграл (1) с заданной точностью <tex>\epsilon >0</tex> путем автоматического выбора шага интегрирования <tex>h_i</tex>. Пусть используется составная квадратурная формула
| |
| - |
| |
| - | <p align="center"><tex>I\approx I_h=\sum_{i=1}^N{I_{h,i}}</tex></p>
| |
| - |
| |
| - | где <tex>I_{h,i}</tex> - квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций). Проведем на каждом частичном отрезке <tex>[x_{i-1},x_i]</tex> все вычисления дважды, один раз - с шагом <tex>h_i</tex> и второй раз - с шагом <tex>0.5h_i</tex> и оценим погрешность по правилу Рунге (17).
| |
| - |
| |
| - | Если для заданного <tex>\epsilon >0</tex> будут выполняться неравенства
| |
| - |
| |
| - | {{ eqno | 18 }}
| |
| - | <p align="center"><tex>|I_i-I_{h/2,i}|\approx \frac{|I_{h/2,i}-I_{h,i}|}{2^m-1} \le \frac{\epsilon h_i}{b-a},i=1,2,...,N,</tex></p>
| |
| - |
| |
| - | то получим
| |
| - |
| |
| - | <p align="center"><tex>|I-I_h/2|\le \frac{\epsilon}{b-a}\sum_{i=1}^N{h,i}=\epsilon,</tex></p>
| |
| - |
| |
| - | т.е. будет достигнута заданная точность <tex>\epsilon</tex>.
| |
| - |
| |
| - | Если же на каком-то из частичных отрезков оценка (18) не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Измельчение сетки на данном отрезке следует проводить до тех пор, пока не будет достигнута оценка вида (18). Заметим, что для некоторой функции <tex>f(x)</tex> такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений,а также вожможность увеличения <tex>\epsilon</tex>.
| |
| - |
| |
| - | Таким образом, автоматический выбор шага интегрирования приводит к тому, что интегрирование ведется с крупным шагом на участках плавного изменения функции <tex>f(x)</tex> и с мелким шагом - на участках быстрого изменения <tex>f(x)</tex>. Это позволяет при заданной точности <tex>\epsilon</tex> уменьшить количество вычислений значений <tex>f(x)</tex> по сравнению с расчетом на сетке с постоянным шагом. Подчеркнем, что для нахождения сумм <tex>I_{h/2,i}</tex> не надо пересчитывать значения <tex>f(x)</tex> во всех узлах, достаточно вычислять <tex>f(x)</tex> только в новых узлах.
| |
| | | | |
| | == Заключение == | | == Заключение == |
Версия 19:46, 13 октября 2008
Введение
Постановка математической задачи
Одной из значения функции ) , равные
, равные =y_0,\cdots,y(x_i)=y_i,\cdots,y(x_n)=y_n) . Требуется построить иносновных задач численного анализа является задача об интерполяции функций.
Пусть на отрезке
. Требуется построить иносновных задач численного анализа является задача об интерполяции функций.
Пусть на отрезке 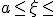 задана сетка
задана сетка 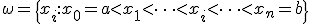 и в её узлах заданы
терполянту — функцию
и в её узлах заданы
терполянту — функцию ) , совпадающую с функцией
, совпадающую с функцией ) в узлах сетки:
в узлах сетки:
( 1 )
=y_i, i=0,1,\cdots,n.)
Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений ) для значений
для значений 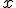 , не содержащихся в таблице данных.
, не содержащихся в таблице данных.
Интерполируюшие функции ) , как правило строятся в виде линейных комбинаций некоторых элементарных функций:
, как правило строятся в виде линейных комбинаций некоторых элементарных функций:
=\sum_{k=0}^N {c_k\Phi_k(x)},)
где \}) — фиксированный линейно независимые функции,
— фиксированный линейно независимые функции, 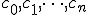 — не определенные пока коэффициенты.
— не определенные пока коэффициенты.
Из условия (1) получаем систему из 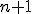 уравнений относительно коэффициентов
уравнений относительно коэффициентов 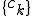 :
:
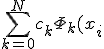}=y_i, i=0,1,\cdots,n.)
Предположим, что система функций ) такова, что при любом выборе узлов
такова, что при любом выборе узлов 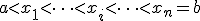 отличен от нуля определитель системы:
отличен от нуля определитель системы:
 = \begin{vmatrix} \Phi_0(x_0) & \Phi_1(x_0) & \cdots & \Phi_n(x_0) \\\Phi_0(x_1) & \Phi_1(x_1) & \cdots & \Phi_n(x_1)\\ \cdots & \cdots & \cdots & \cdots \\\Phi_0(x_n) & \Phi_1(x_n) & \cdots & \Phi_n(x_n)\end{vmatrix}) .
.
Тогда по заданным ) однозначно определяются коэффициенты
однозначно определяются коэффициенты ) .
.
Изложение метода
Интерполяция кубическими сплайнами является частным случаем кусочно-полиномиальной интерполцией. В этом специальном случае между любыми двумя соседними узлами функция интерполируется кубическим полиномом. его коэффициенты на каждом интервале определяются из условий сопряжения в узлах:
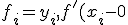=f'(x_i+0),
f''(x_i-0)=f''(x_i+0), i=1, 2, \cdots, n-1.)
Кроме того, на границе при 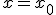 и
и 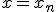 ставятся условия
ставятся условия
( 2 )
=0, f''(x_n)=0.)
Будем искать кубический полином в виде
( 3 )
=a_i+b_i(x-x_{i-1})+c_i(x-x_{i-1})^2+d_i(x-x_{i-1})^3, x_{i-1}\le \x\le \x_i.)
Из условия 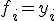 имеем
имеем
( 4 )
=a_i=y_{i-1},
f(x_i)=a_i+b_ih_i+c_ih_i^2+d_ih_i^3=y_i,
h_i=x_i-x_{i-1}, i=1, 2, \cdots, n-1.)
Вычислим производные:
=b_i+2c_i(x-x_{i-1})+3d_i(x-x_{i-1})^2,
f''(x)=2c_i+6d_i(x-x_{i-1}), x_{i-1}\le \x\le \x_i,)
и потребуем их непрерывности при 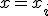 :
:
( 5 )
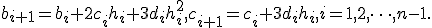
Общее число неизвестных коэффициентов, очевидно, равно 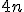 , число уравнений (4) и (5) равно
, число уравнений (4) и (5) равно 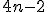 . Недостающие два уравнения получаем из условия (2) при
. Недостающие два уравнения получаем из условия (2) при 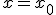 и
и 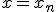 :
:
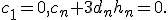
Выражение из (5) 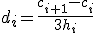 , подставляя это выражение в (4) и исключая
, подставляя это выражение в (4) и исключая 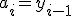 , получим
, получим
![b_i=\[\frac{y_i-y_{i-1}}h_i\]-\frac{1}{3}h_i(c_{i+1}+2c_i), i=1, 2, \cdots, n-1,
b_n=\[\frac{y_n-y_{n-1}}h_n\]-\frac{2}{3}h_nc_n,.](../mimetex/?b_i=\[\frac{y_i-y_{i-1}}h_i\]-\frac{1}{3}h_i(c_{i+1}+2c_i), i=1, 2, \cdots, n-1,
b_n=\[\frac{y_n-y_{n-1}}h_n\]-\frac{2}{3}h_nc_n,.)
Подставив теперь выражения для 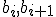 и
и 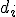 в первую формулу (5), после несложных преобразований получаем для определения
в первую формулу (5), после несложных преобразований получаем для определения 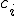 разностное уравнение второго порядка
разностное уравнение второго порядка
( 6 )
c_{i+1}+h_{i+1}c_{i+2}=s\left(\frac{y_{i+1}-y_i}{h_{i+1}} - \frac{y_{i+1}-y_i}{h_{i+1}}\right), i=1, 2, \cdots, n-1.)
С краевыми условиями
( 7 )
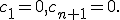
Условие 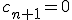 эквивалентно условию
эквивалентно условию 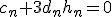 и уравнению
и уравнению 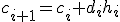 . Разностное уравнение (6) с условиями (7) можно решить методом прогонки, представив в виде системы линейных алгебраических уравнений вида
. Разностное уравнение (6) с условиями (7) можно решить методом прогонки, представив в виде системы линейных алгебраических уравнений вида 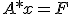 , где вектор
, где вектор 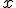 соответствует вектору
соответствует вектору 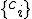 , вектор
, вектор 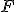 поэлементно равен правой части уравнения (6), а матрица
поэлементно равен правой части уравнения (6), а матрица 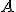 имеет следующий вид:
имеет следующий вид:

где  и
и , i =1, \cdots, n) .
.
Метод прогонки
Метод прогонки, основан на предположении, что искомые неизвестные связаны рекуррентным соотношением:
( 8 )
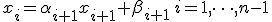
Используя это соотношение, выразим 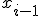 и
и 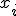 через
через 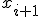 и подставим
и подставим
в i-e уравнение:
x_{i+1} + A_i\alpha_i\beta_{i+1} + A_i\beta_i + C_i\beta_{i+1} - F_i = 0
)
,
где 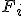 - правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать
- правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать
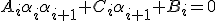
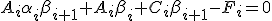
Отсюда следует:
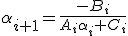
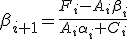
Из первого уравнения получим:
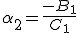
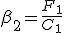
После нахождения прогоночных коэффициентов 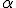 и
и 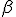 , используя уравнение (1), получим решение системы. При этом,
, используя уравнение (1), получим решение системы. При этом,
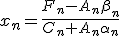
Числовой пример
Построим интерполянту для для функции  xtex>
! f(x)" alt= "ftex> заданой следующим образом:
{| class="wikitable"
|-
! xtex>
! f(x)" />
|-
| 1
| 1.0002
|-
| 2
| 1.0341
|-
| 3
| 0.6
|-
| 4
| 0.40105
|-
| 5
| 0.1
|-
| 6
| 0.23975
|}
xtex>
! f(x)" alt= "ftex> заданой следующим образом:
{| class="wikitable"
|-
! xtex>
! f(x)" />
|-
| 1
| 1.0002
|-
| 2
| 1.0341
|-
| 3
| 0.6
|-
| 4
| 0.40105
|-
| 5
| 0.1
|-
| 6
| 0.23975
|}
Рекомендации программисту
Заключение
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы М.: Наука, 1989.
- А.А.Самарский. Введение в численные методы М.: Наука, 1982.
- Костомаров Д.П., Фаворский А.П. Вводные лекции по численным методам
, равные
. Требуется построить иносновных задач численного анализа является задача об интерполяции функций.
Пусть на отрезке
задана сетка
и в её узлах заданы
терполянту — функцию
, совпадающую с функцией
в узлах сетки:
для значений
, не содержащихся в таблице данных.
, как правило строятся в виде линейных комбинаций некоторых элементарных функций:
— фиксированный линейно независимые функции,
— не определенные пока коэффициенты.
уравнений относительно коэффициентов
:
такова, что при любом выборе узлов
отличен от нуля определитель системы:
.
однозначно определяются коэффициенты
.
и
ставятся условия
имеем
:
, число уравнений (4) и (5) равно
. Недостающие два уравнения получаем из условия (2) при
и
:
, подставляя это выражение в (4) и исключая
, получим
и
в первую формулу (5), после несложных преобразований получаем для определения
разностное уравнение второго порядка
эквивалентно условию
и уравнению
. Разностное уравнение (6) с условиями (7) можно решить методом прогонки, представив в виде системы линейных алгебраических уравнений вида
, где вектор
соответствует вектору
, вектор
поэлементно равен правой части уравнения (6), а матрица
имеет следующий вид:
и
.
и
через
и подставим
- правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать
и
, используя уравнение (1), получим решение системы. При этом,
xtex>
!

