Алгоритм LOWESS
Материал из MachineLearning.
(→Введение) |
|||
| (9 промежуточных версий не показаны.) | |||
| Строка 5: | Строка 5: | ||
: Данная методика была предложена Кливлендом(Cleveland) в 1979 году для моделирования и сглаживания двумерных данных <tex> X^m={(x_i, y_i)}_{i=1}^m</tex>. Эта техника предоставляет общий и гибкий подход для приближения двумерных данных. | : Данная методика была предложена Кливлендом(Cleveland) в 1979 году для моделирования и сглаживания двумерных данных <tex> X^m={(x_i, y_i)}_{i=1}^m</tex>. Эта техника предоставляет общий и гибкий подход для приближения двумерных данных. | ||
| - | : Локально-линейная модель loess(lowess) | + | : '''Локально-линейная модель''' loess(lowess) может быть записана в виде: |
:: <tex> y_t=\alpha_t+\beta_t x_t + \varepsilon_t.</tex> | :: <tex> y_t=\alpha_t+\beta_t x_t + \varepsilon_t.</tex> | ||
| - | : Эта модель может быть '''расширена''' на случай '''локально-квадратичной зависимости'' и на модель с '''бо‘льшим числом независимых переменных'''. | + | : Эта модель может быть '''расширена''' на случай '''локально-квадратичной зависимости''' и на модель с '''бо‘льшим числом независимых переменных'''. |
| - | : Параметры <tex>\alpha_t</tex> и <tex>\beta_t</tex> локально линейной модели оцениваются | + | : Параметры <tex>\alpha_t</tex> и <tex>\beta_t</tex> локально линейной модели оцениваются с помощью локально взвешенной регрессии, которая присваивает объекту тем больший вес, чем более близок он к объекту <tex>t</tex>. |
:Степень сглаживания определяется '''параметром сглаживания''' <tex>f</tex>, который выбирает пользователь. | :Степень сглаживания определяется '''параметром сглаживания''' <tex>f</tex>, который выбирает пользователь. | ||
| - | : Параметр <tex>f</tex> '''указывает какая доля(fraction) данных''' используется в процедуре. Если <tex>f = 0.5</tex>, то только половина данных используется для оценки и влияет на результат, и тогда мы получим умеренное сглаживание. С другой стороны, если <tex>f = 0.8</tex>, то используются восемьдесят процентов данных, и сглаживание намного сильнее. Во всех случаях веса данных тем больше чем они ближе к объекту <tex>t</tex>. | + | : Параметр <tex>f</tex> '''указывает, какая доля (fraction) данных''' используется в процедуре. Если <tex>f = 0.5</tex>, то только половина данных используется для оценки и влияет на результат, и тогда мы получим умеренное сглаживание. С другой стороны, если <tex>f = 0.8</tex>, то используются восемьдесят процентов данных, и сглаживание намного сильнее. Во всех случаях веса данных тем больше, чем они ближе к объекту <tex>t</tex>. |
| - | : Процедура оценки использует '''не''' метод наименьших квадратов, а более устойчивый(робастный) метод, который принимает меры против выбросов. | + | : Процедура оценки использует '''не''' метод наименьших квадратов, а более устойчивый ( робастный ) метод, который принимает меры против выбросов. |
:График приближенных значений | :График приближенных значений | ||
:: <tex> \hat{y_t}=\hat{\alpha_t}+\hat{\beta_t}x_t </tex> | :: <tex> \hat{y_t}=\hat{\alpha_t}+\hat{\beta_t}x_t </tex> | ||
| - | :от <tex>x_t</tex> '''полезен для принятия решения о характере связи между <tex>y_t</tex> и <tex>x_t</tex>'''. Для проверки качества приближения полученного с помощью процедуры устойчивого loess полезно посмотреть на график остатков обычной | + | :от <tex>x_t</tex> '''полезен для принятия решения о характере связи между <tex>y_t</tex> и <tex>x_t</tex>'''. Для проверки качества приближения полученного с помощью процедуры устойчивого loess полезно посмотреть на график остатков обычной регрессии, то есть в осях '''(i)''' остатки от числа наблюдения '''(ii)''' остатки от прибли‘женных значений, '''(iii)''' остатки от значений независимой переменной. Как показал Кливленд, может быть предпочтительно использовать график в осях модули остатков от полученных приближенных значений вместо графика '''(ii)''' для устойчивого loess сглаживания, чтобы проверить наличие тренда или других систематических особенностей. |
| - | :Когда <tex>m > 100</tex> вычисления могут быть слишком долгими, в этом случае можно сократить количество вычислений оценивая <tex>\hat{\alpha_t}</tex> и <tex>\hat{\beta_t}</tex> только в точках отстоящих друг от друга как минимум на <tex>\delta</tex> единиц, где параметр <tex>\delta</tex> может задаваться либо приниматься по умолчанию. Рекомендуемые значения | + | :Когда <tex>m > 100</tex> вычисления могут быть слишком долгими, в этом случае можно сократить количество вычислений, оценивая <tex>\hat{\alpha_t}</tex> и <tex>\hat{\beta_t}</tex> только в точках отстоящих друг от друга как минимум на <tex>\delta</tex> единиц, где параметр <tex>\delta</tex> может задаваться либо приниматься по умолчанию. Рекомендуемые значения |
| - | :: <tex>\delta=0, </tex> | + | :: <tex>\delta=0, </tex> если <tex>m <= 100 </tex> |
| - | :: <tex>\delta=0.03*IQR,</tex> | + | :: <tex>\delta=0.03*IQR,</tex> если <tex>m > 100</tex>, где <tex>IQR</tex> — ['''межквартильный размах'''](Interquartile range). |
:С такими параметрами вычисления будут выполнены для примерно 100 точек. | :С такими параметрами вычисления будут выполнены для примерно 100 точек. | ||
| - | ===Примеры=== | + | === Примеры === |
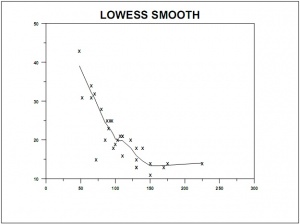
[[Изображение:Loess_f_s.jpg|thumb|Рис. 2. Задание параметра сглаживания <tex>f</tex>|300px]] | [[Изображение:Loess_f_s.jpg|thumb|Рис. 2. Задание параметра сглаживания <tex>f</tex>|300px]] | ||
:На '''Рис. 2'''. Приведена иллюстрация уровня сглаживания в зависимости от значения параметра <tex>f</tex> | :На '''Рис. 2'''. Приведена иллюстрация уровня сглаживания в зависимости от значения параметра <tex>f</tex> | ||
| Строка 38: | Строка 38: | ||
Базовое предположение состоит в следующем | Базовое предположение состоит в следующем | ||
::<tex>y_t=g(x_t)+\varepsilon_t , t=1,\ldots,m</tex> | ::<tex>y_t=g(x_t)+\varepsilon_t , t=1,\ldots,m</tex> | ||
| - | где <tex>g(x)</tex> - функция | + | где <tex>g(x)</tex> - функция сглаживания, остатки <tex>\varepsilon_t</tex> имеют нулевое математическое ожидание и фиксированную дисперсию. Затем сглаживание <tex>g</tex> мы приближаем локально-линейной (локально квадратичной, в случае нелинейной модели) функцией, чтобы получить |
:: <tex> y_t=\alpha_t + \beta_t x_t + \varepsilon_t</tex>. | :: <tex> y_t=\alpha_t + \beta_t x_t + \varepsilon_t</tex>. | ||
| - | Для четкого определения | + | Для четкого определения алгоритма поясним концепцию '''локальных весов''' <tex>w(x_t)</tex> и '''робастных весов''' <tex>\delta(x_t)</tex>. |
=== Локальные веса === | === Локальные веса === | ||
:Рассмотрим один из широко распространенных примеров – функцию | :Рассмотрим один из широко распространенных примеров – функцию | ||
| Строка 61: | Строка 61: | ||
==== Замечание ==== | ==== Замечание ==== | ||
| - | :Возможны и другие варианты выбора весов <tex>\delta_t</tex>, например, занулить <tex>p</tex> штук, соответствующих наибольшим <tex>\hat{\varepsilon_t}</tex>. Это | + | :Возможны и другие варианты выбора весов <tex>\delta_t</tex>, например, занулить <tex>p</tex> штук, соответствующих наибольшим <tex>\hat{\varepsilon_t}</tex>. Это соответствует ядру |
::<tex>\bar{K}(z)=[z<\hat{\varepsilon}^{(m-p)}],</tex> | ::<tex>\bar{K}(z)=[z<\hat{\varepsilon}^{(m-p)}],</tex> | ||
где <tex>\hat{\varepsilon}^{(m-p)}</tex> –- <tex>(m-p)</tex> - тый член вариационного ряда <tex>\hat{\varepsilon}^{(1)}<=\ldots<=\hat{\varepsilon}^{(m)}</tex> | где <tex>\hat{\varepsilon}^{(m-p)}</tex> –- <tex>(m-p)</tex> - тый член вариационного ряда <tex>\hat{\varepsilon}^{(1)}<=\ldots<=\hat{\varepsilon}^{(m)}</tex> | ||
:В качестве весовой ядерной функции можно взять функцию Хубера (Huber, 1964) на которой основаны *[M-оценки] | :В качестве весовой ядерной функции можно взять функцию Хубера (Huber, 1964) на которой основаны *[M-оценки] | ||
<tex>K(z)= \left{ z^2, \, \, \, |z| \le c\\ 2c|z|-c_2, \, \, \, |z|>c \right. </tex> | <tex>K(z)= \left{ z^2, \, \, \, |z| \le c\\ 2c|z|-c_2, \, \, \, |z|>c \right. </tex> | ||
| - | Чтобы вычислить <tex>K(z)</tex> необходимо выбрать параметр устойчивости <tex>c</tex>. Одно популярное прикладное правило – <tex>c = 1,345 | + | Чтобы вычислить <tex>K(z)</tex> необходимо выбрать параметр устойчивости <tex>c</tex>. Одно популярное прикладное правило – <tex>c = 1,345 * s</tex> , где <tex>s</tex> – '''робастная мера масштаба''', такая как медианное абсолютное отклонение от медианы (MAD). Это популярное правило обеспечивает 95%-ую эффективность относительно гомоскедастичной нормальной модели в проблеме местоположения. |
=== Алгоритм LOWESS === | === Алгоритм LOWESS === | ||
| Строка 78: | Строка 78: | ||
==== Алгоритм 1.1==== | ==== Алгоритм 1.1==== | ||
| - | :'''1.''' Построить | + | :'''1.''' Построить линейную регрессию во всех <tex>t=1,\ldots,t=m</tex> точках, используя весовые функции <tex>w_t</tex>, тем самым получим оценки для параметров модели <tex>\hat{\alpha_t}, \hat{\beta_t}</tex>. |
:А также приближения <tex>\hat{y_t}=\hat{\alpha_t}+\hat{\beta_t}x_t</tex>. | :А также приближения <tex>\hat{y_t}=\hat{\alpha_t}+\hat{\beta_t}x_t</tex>. | ||
:'''2.''' Инициализируем остатки <tex>\hat{\varepsilon_t}= \| \hat{y_t} - y_t \|</tex>. Вычислим робастные веса <tex>\delta_t =\bar{K}(\hat{\varepsilon_t})</tex> | :'''2.''' Инициализируем остатки <tex>\hat{\varepsilon_t}= \| \hat{y_t} - y_t \|</tex>. Вычислим робастные веса <tex>\delta_t =\bar{K}(\hat{\varepsilon_t})</tex> | ||
:'''3.''' '''повторять''' | :'''3.''' '''повторять''' | ||
| - | ::'''4.''' Построить | + | ::'''4.''' Построить линейную регрессию во всех <tex>t=1,\ldots,t=m</tex> точках, используя весовые функции <tex>\delta_t w_t</tex>, тем самым получим оценки для параметров модели <tex>\hat{\alpha_t}, \hat{\beta_t}</tex>. А также приближения <tex>\hat{y_t}=\hat{\alpha_t}+\hat{\beta_t}x_t</tex>. |
::'''5.''' По новому набору значений <tex>\hat{\varepsilon_t}= \| \hat{y_t} - y_t \|</tex> вычислить новые значения коэффициентов <tex>\delta_t =\bar{K}(\hat{\varepsilon_t})</tex>. | ::'''5.''' По новому набору значений <tex>\hat{\varepsilon_t}= \| \hat{y_t} - y_t \|</tex> вычислить новые значения коэффициентов <tex>\delta_t =\bar{K}(\hat{\varepsilon_t})</tex>. | ||
:'''6.''' '''пока''' веса <tex>\delta_t</tex> не стабилизируются | :'''6.''' '''пока''' веса <tex>\delta_t</tex> не стабилизируются | ||
| Строка 100: | Строка 100: | ||
в свою очередь, зависит от <tex>\delta_t</tex>. На каждой итерации строится функция <tex>a</tex>, | в свою очередь, зависит от <tex>\delta_t</tex>. На каждой итерации строится функция <tex>a</tex>, | ||
затем уточняются весовые множители <tex>\delta_t</tex>. Как правило, этот процесс сходится довольно быстро. | затем уточняются весовые множители <tex>\delta_t</tex>. Как правило, этот процесс сходится довольно быстро. | ||
| - | '''Однако в практических реализациях имеет смысл вводить ограничение на количество итераций, как правило это 2-3 итерации'''. | + | '''Однако в практических реализациях имеет смысл вводить ограничение на количество итераций, как правило, это 2-3 итерации'''. |
== Примеры== | == Примеры== | ||
| Строка 108: | Строка 108: | ||
'''Конечно, подход вычислительно достаточно требовательный, однако этот метод заслуживает внимания тех исследователей, которые обеспокоены наличием выбросов в данных. В частности он активно применяется в биологии в области генетических исследований.''' | '''Конечно, подход вычислительно достаточно требовательный, однако этот метод заслуживает внимания тех исследователей, которые обеспокоены наличием выбросов в данных. В частности он активно применяется в биологии в области генетических исследований.''' | ||
| - | ==Литература== | + | == Литература == |
# {{книга | # {{книга | ||
| Строка 146: | Строка 146: | ||
|издательство = Квантиль, №4, стр. 7–56. | |издательство = Квантиль, №4, стр. 7–56. | ||
|год = 2008 | |год = 2008 | ||
| + | }} | ||
| + | # {{книга | ||
| + | |автор = Huber, P.J. | ||
| + | |заглавие = Robust estimation of a location parameter. Annals of Statistics 35 | ||
| + | |страницы = 73–101 | ||
| + | |год = 1964 | ||
}} | }} | ||
| Строка 153: | Строка 159: | ||
* [http://en.wikipedia.org/wiki/Local_regression Local regression] | * [http://en.wikipedia.org/wiki/Local_regression Local regression] | ||
| - | [[Категория: | + | [[Категория:Непараметрическая регрессия]] |
| - | + | [[Категория:Робастная регрессия]] | |
| - | + | ||
| - | + | ||
Текущая версия
Содержание |
Введение
- Данная методика была предложена Кливлендом(Cleveland) в 1979 году для моделирования и сглаживания двумерных данных
. Эта техника предоставляет общий и гибкий подход для приближения двумерных данных.
- Локально-линейная модель loess(lowess) может быть записана в виде:
-
- Эта модель может быть расширена на случай локально-квадратичной зависимости и на модель с бо‘льшим числом независимых переменных.
- Параметры
и
локально линейной модели оцениваются с помощью локально взвешенной регрессии, которая присваивает объекту тем больший вес, чем более близок он к объекту
.
- Степень сглаживания определяется параметром сглаживания
, который выбирает пользователь.
- Параметр
указывает, какая доля (fraction) данных используется в процедуре. Если
, то только половина данных используется для оценки и влияет на результат, и тогда мы получим умеренное сглаживание. С другой стороны, если
, то используются восемьдесят процентов данных, и сглаживание намного сильнее. Во всех случаях веса данных тем больше, чем они ближе к объекту
.
- Процедура оценки использует не метод наименьших квадратов, а более устойчивый ( робастный ) метод, который принимает меры против выбросов.
- График приближенных значений
-
- от
полезен для принятия решения о характере связи между
и
. Для проверки качества приближения полученного с помощью процедуры устойчивого loess полезно посмотреть на график остатков обычной регрессии, то есть в осях (i) остатки от числа наблюдения (ii) остатки от прибли‘женных значений, (iii) остатки от значений независимой переменной. Как показал Кливленд, может быть предпочтительно использовать график в осях модули остатков от полученных приближенных значений вместо графика (ii) для устойчивого loess сглаживания, чтобы проверить наличие тренда или других систематических особенностей.
- Когда
вычисления могут быть слишком долгими, в этом случае можно сократить количество вычислений, оценивая
и
только в точках отстоящих друг от друга как минимум на
единиц, где параметр
может задаваться либо приниматься по умолчанию. Рекомендуемые значения
-
если
-
если
, где
— [межквартильный размах](Interquartile range).
-
- С такими параметрами вычисления будут выполнены для примерно 100 точек.
Примеры
- На Рис. 2. Приведена иллюстрация уровня сглаживания в зависимости от значения параметра
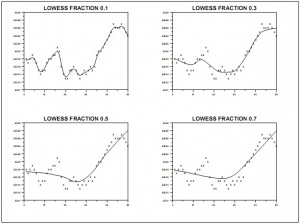
- Сглаживание также может быть локально квадратичным, в этом случае модель для
имеет вид
-
Примеры сглаживания с квадратичным локальным приближением показаны на Рис. 3.
Технические детали алгоритма
Базовое предположение состоит в следующем
где - функция сглаживания, остатки
имеют нулевое математическое ожидание и фиксированную дисперсию. Затем сглаживание
мы приближаем локально-линейной (локально квадратичной, в случае нелинейной модели) функцией, чтобы получить
-
.
-
Для четкого определения алгоритма поясним концепцию локальных весов и робастных весов
.
Локальные веса
- Рассмотрим один из широко распространенных примеров – функцию
- Для заданного параметра
пусть
- ближайшее целое число к произведению
. Пусть
расстояние до
-того ближайшего соседа объекта
. Тогда локальный вес для любого объекта
в окрестности
есть
.
Замечание
- Более общий подход к определению локальных весов состоит в выборе ширины окна
, в общем случае
, то есть зависящей от объекта
, и ядровой функции
. Тогда локальные веса вычисляются по формулам
- В этом случае отпадает необходимость задания параметра сглаживания
и его смысл эквивалентен выбору ширины окна
.
Робастные веса
Пусть
– обучающая выборка за исключением элемента
,
– ответ алгоритма
, обученного на выборке
при работе на объекте
.
– ошибка алгоритма на объекте
(ошибка скользящего контроля).
Пусть - есть медиана величин
.
тогда
, где
Замечание
- Возможны и другие варианты выбора весов
, например, занулить
штук, соответствующих наибольшим
. Это соответствует ядру
где –-
- тый член вариационного ряда
- В качестве весовой ядерной функции можно взять функцию Хубера (Huber, 1964) на которой основаны *[M-оценки]
Чтобы вычислить
необходимо выбрать параметр устойчивости
. Одно популярное прикладное правило –
, где
– робастная мера масштаба, такая как медианное абсолютное отклонение от медианы (MAD). Это популярное правило обеспечивает 95%-ую эффективность относительно гомоскедастичной нормальной модели в проблеме местоположения.
Алгоритм LOWESS
Вход
- обучающая выборка;
весовые функции;
Выход
Коэффициенты
Алгоритм 1.1
- 1. Построить линейную регрессию во всех
точках, используя весовые функции
, тем самым получим оценки для параметров модели
.
- А также приближения
.
- 2. Инициализируем остатки
. Вычислим робастные веса
- 3. повторять
- 4. Построить линейную регрессию во всех
точках, используя весовые функции
, тем самым получим оценки для параметров модели
. А также приближения
.
- 5. По новому набору значений
вычислить новые значения коэффициентов
.
- 4. Построить линейную регрессию во всех
- 6. пока веса
не стабилизируются
При использовании ядровых функций для оценки локальных весов объектов и робастных весов алгоритм модифицируется следующим образом:
Алгоритм 1.2
- 1. Инициализировать
- 2. повторять
- 3. Вычислить оценки скользящего контроля на каждом объекте
-
- 4. По набору значений
вычислить новые значения коэффициентов
.
- 5. пока веса
не стабилизируются
Коэффициенты , как и ошибки
, зависят от функции
, которая,
в свою очередь, зависит от
. На каждой итерации строится функция
,
затем уточняются весовые множители
. Как правило, этот процесс сходится довольно быстро.
Однако в практических реализациях имеет смысл вводить ограничение на количество итераций, как правило, это 2-3 итерации.
Примеры
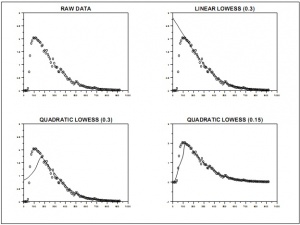
- На рисунке 4 представлен пример робастного локально-линейного сглаживания с помощь алгоритма LOWESS. С числом итераций цикла равным 2 и параметром сглаживания
, то есть для приближения используется
ближайших точек выборки.
Конечно, подход вычислительно достаточно требовательный, однако этот метод заслуживает внимания тех исследователей, которые обеспокоены наличием выбросов в данных. В частности он активно применяется в биологии в области генетических исследований.
Литература
- A.I. McLeod Statistics 259b Robust Loess: S lowess. — 2004.
- Хардле В. Прикладная непараметрическая регрессия.. — Мир, 1993.
- Воронцов К.В. Лекции по алгоритмам восстановления регрессии. — 2007.
- John A Berger, Sampsa Hautaniemi, Anna-Kaarina Järvinen, Henrik Edgren, Sanjit K Mitra and Jaakko Astola Optimized LOWESS normalization parameter selection for DNA microarray data. — BMC Bioinformatics, 2004.
- Maronna, A., R. Martin, V. Yohai Robust Statistics: Theory and Methods.. — Wiley, 2006.
- Расин, Джеффри «Непараметрическая эконометрика: вводный курс». — Квантиль, №4, стр. 7–56., 2008.
- Huber, P.J. Robust estimation of a location parameter. Annals of Statistics 35. — 1964. — С. 73–101.