Прореживание двухслойной нейронной сети (пример)
Материал из MachineLearning.
(→Настройка нейронной сети) |
(→Исходный код) |
||
| (25 промежуточных версий не показаны.) | |||
| Строка 6: | Строка 6: | ||
== Настройка нейронной сети == | == Настройка нейронной сети == | ||
[[Изображение:Something.jpg|500px]] <br /> | [[Изображение:Something.jpg|500px]] <br /> | ||
| - | Двухслойная нейронная сеть состоит из одного скрытого слоя и выходного слоя. Входной слой - это объект со своим признаковым описанием <tex>x_1, ... , x_n</tex>. Первый и второй слои сети состоят из так называемых [[ | + | Двухслойная нейронная сеть состоит из одного скрытого слоя и выходного слоя. Входной слой - это объект со своим признаковым описанием <tex>x_1, ... , x_n</tex>. Первый и второй слои сети состоят из так называемых нейронов, или [[Персептрон|персептронов]]. Каждый нейрон вычисляет <tex>n</tex>-арную функцию вида <tex>a(x) = \phi (<w,x>)</tex>. В нашем случае <tex>\phi</tex> - сигмоидальная функция активации <tex>\phi(z) = 1 / (1 + e^{-z})</tex>. Значения признаков <tex>x_i</tex> поступают на вход первому (скрытому) слою сети с весовой матрицей <tex>W_1</tex>, выходы первого слоя поступают на вход второму с весовой матрицей <tex>W_2</tex>.На выходе второго слоя вычисляется вектор-функция <tex>\bf{F} = (F_1(x),...,F_P(x))</tex>, где <tex>P</tex> - количество нейронов на втором слое. Необходимо настроить параметры сети, используя алгоритм обратного распространения (back propagation). <br />Введем функции ошибок: <tex>\bf{E}(\bf{w}) = \frac{1}{2N} \sum_{n = 1}^N \sum_{p = 1}^P(F_p(n) - Y_p(n))^2</tex> - нормированная среднеквадратичная ошибка, <tex>\bf{E}(n) = \frac{1}{2}\sum_{p = 1}^P (F_p(n) - y_p(n))^2</tex> - ошибка на конкретном объекте. Пусть <tex>w_{ji}</tex> - вес, соединяющий нейрон <tex>i </tex> с нейроном <tex>j</tex> следующего слоя. Тогда коррекция веса, применяемая к <tex>w_{ji}(n)</tex>, определяется согласно правилу <tex>\Delta w_{ji} = \eta \bf{\delta}_j(n)y_i(n)</tex>, где <tex>\bf{\delta}_j(n) = - \frac{\partial \bf{E}(n)}{\partial y_j(n)}\phi_j'(v_j(n))</tex> - локальный градиент нейрона <tex>j</tex>. Здесь <tex>y_i(n)</tex> - выход <tex>i</tex>-го нейрона, <tex>v_j(n) = \sum_{i = 1}^m w_{ji}(n)y_i(n)</tex> - значение, которое получает на вход функция активации, соответствующая <tex>j</tex>-му нейрону (<tex>m</tex> - количество его входов), <tex>\eta</tex> - темп обучения. Для выходного слоя <tex>\frac {\partial \bf{E}(n)}{\partial y_j(n)} = y_j(n) - F_j(n) =: e_j(n)</tex>, и для него справедливо <tex>\Delta w_{ji} = - \eta e_j(n)\phi_j'(v_j(n))y_i(n)</tex>. |
| - | Соответственно, для первого, скрытого, слоя справедлива формула обратного распространения <tex>\delta_j(n) = \phi_j'(v_j(n)) \sum_{p = 1}^P \delta_p(n) w_{pj}(n) </tex>. | + | Соответственно, для первого, скрытого, слоя справедлива формула обратного распространения <tex>\delta_j(n) = \phi_j'(v_j(n)) \sum_{p = 1}^P \delta_p(n) w_{pj}(n) </tex>. <br /> <br /> |
| + | Отметим, что эти формулы взяты из книги С. Хайкина "Нейронные сети. Полный курс". | ||
== Алгоритм оптимального прореживания == | == Алгоритм оптимального прореживания == | ||
Описание метода второго порядка приводится в статье [[Оптимальное прореживание нейронных сетей]]. <br /> | Описание метода второго порядка приводится в статье [[Оптимальное прореживание нейронных сетей]]. <br /> | ||
| + | Локальная аппроксимация функции ошибки в окрестности стационарного положения: <tex>E(\mathbf{w}+\Delta\mathbf{w}) = E(\mathbf{w}) + \mathbf{g}^T(\mathbf{w})\Delta\mathbf{w} + \frac{1}{2}\Delta\mathbf{w}^TH\Delta\mathbf{w} +o(\|\mathbf{w}\|^3),</tex> | ||
| + | где <tex>\Delta \mathbf{w}</tex> — возмущение вектора параметров <tex>\mathbf{w}</tex>, <tex>\mathbf{g}</tex> — градиент <tex>\frac{\partial E}{\partial \mathbf{w}}</tex>, | ||
| + | и <tex>H=H(\mathbf{w})</tex> — матрица вторых производных <tex>\frac{\partial^2 E}{\partial \mathbf{w}^2}</tex>. <br /> | ||
Необходимо минимизировать квадратичную форму <tex>\Delta E = \frac{1}{2}\Delta \bf{w}^T\bf{H}\Delta \bf{w}</tex> по отношению к <tex>\Delta \bf{w}</tex>при ограничении <tex>\bf{e}_i^T \Delta \bf{w} + w_i = 0</tex>. Для решения этой условной задачи строится лагранжиан <tex>S = \frac{1}{2}\Delta \bf{w}^T \bf{H} \Delta \bf{w} - \lambda (\bf{e}_i^T\Delta \bf{w} + w_i)</tex>. Получаем, что оптимальное приращение вектора весов <tex>\Delta\mathbf{w}=-\frac{w_i}{[H^{-1}]_{ii}}H^{-1}\mathbf{e}_i</tex>, а соответствующее ему оптимальное значение лагранжиана для элемента <tex>w_i</tex>: <tex>S_i=\frac{w_i^2}{2[\bf{H}^{-1}]_{ii}}.</tex> | Необходимо минимизировать квадратичную форму <tex>\Delta E = \frac{1}{2}\Delta \bf{w}^T\bf{H}\Delta \bf{w}</tex> по отношению к <tex>\Delta \bf{w}</tex>при ограничении <tex>\bf{e}_i^T \Delta \bf{w} + w_i = 0</tex>. Для решения этой условной задачи строится лагранжиан <tex>S = \frac{1}{2}\Delta \bf{w}^T \bf{H} \Delta \bf{w} - \lambda (\bf{e}_i^T\Delta \bf{w} + w_i)</tex>. Получаем, что оптимальное приращение вектора весов <tex>\Delta\mathbf{w}=-\frac{w_i}{[H^{-1}]_{ii}}H^{-1}\mathbf{e}_i</tex>, а соответствующее ему оптимальное значение лагранжиана для элемента <tex>w_i</tex>: <tex>S_i=\frac{w_i^2}{2[\bf{H}^{-1}]_{ii}}.</tex> | ||
| Строка 33: | Строка 37: | ||
На графике показаны результаты классификации. На первом и втором слое сети - по 5 нейронов, количество признаков - 4. Итого получается 45 весов. Видно, что алгоритм сработал без ошибок.<br /> | На графике показаны результаты классификации. На первом и втором слое сети - по 5 нейронов, количество признаков - 4. Итого получается 45 весов. Видно, что алгоритм сработал без ошибок.<br /> | ||
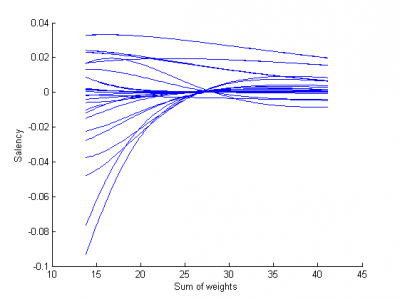
| - | [[Изображение: | + | [[Изображение:iriss2.png|500px]] <br /> Ниже приведены графики функции выпуклости (одная кривая - зависимость функции выпуклости от суммы модулей параметров) и график зависимости ошибки от количества удаленных параметров. |
| - | [[Изображение: | + | [[Изображение:Salency2.png|400px]] |
| - | [[Изображение:OBD2. | + | [[Изображение:OBD2.png|400px]]<br /> |
Видно, что из сети с 45 параметрами можно удалить 18, практически не проиграв в качестве. | Видно, что из сети с 45 параметрами можно удалить 18, практически не проиграв в качестве. | ||
=== Пример 2: выборка линейно неразделима === | === Пример 2: выборка линейно неразделима === | ||
| - | Те же самые 45 весов. Алгоритм допустил | + | Те же самые 45 весов. Алгоритм допустил 4 ошибки при классификации: |
| - | [[Изображение: | + | [[Изображение:Iriss.png|500px]]<br /> |
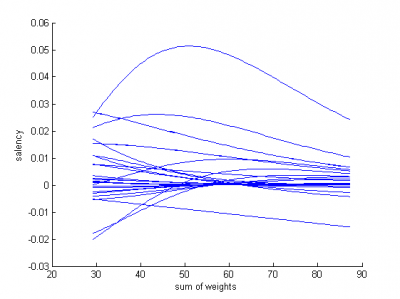
Графики функции выпуклости и количества ошибок: <br /> | Графики функции выпуклости и количества ошибок: <br /> | ||
| - | [[Изображение: | + | [[Изображение:Salency1.png|400px]] |
| - | [[Изображение: | + | [[Изображение:OBD1.png|400px]]<br /> |
| - | Результат прореживания здесь более наглядный: можно удалить 35 из 45 параметров без потери качества. | + | Результат прореживания здесь более наглядный: можно удалить 35 из 45 параметров без потери качества. <br /> |
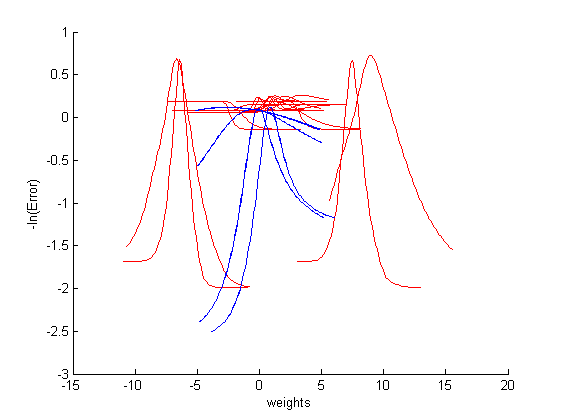
| + | Для этого случая построим график функции ошибки (<tex>-ln E</tex>)в зависимости от параметров. На этом графике красным показаны параметры первого слоя, а синим - второго. В результате применения алгоритма OBD сначала удалялись те параметры, которые на графике видны плохо - именно они не оказывают большого значения на аппроксимацию.<br /> | ||
| + | |||
| + | [[Изображение:Errors.png|600px]]<br /> | ||
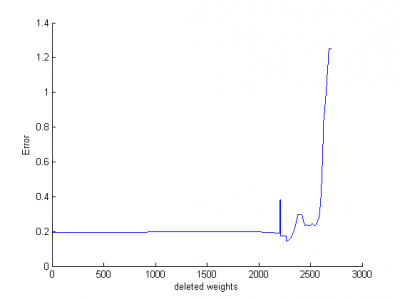
Приведем график зависимости ошибки от количества удаленных параметров для тех же данных и 50 нейронов на каждом из слоев. | Приведем график зависимости ошибки от количества удаленных параметров для тех же данных и 50 нейронов на каждом из слоев. | ||
| - | [[Изображение: | + | [[Изображение:OBD3.png|400px]] |
== Исходный код == | == Исходный код == | ||
| - | Скачать листинги алгоритмов можно здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/ | + | Скачать листинги алгоритмов можно здесь: [https://mlalgorithms.svn.sourceforge.net/svnroot/mlalgorithms/Group774/Kuznetsov2010Thinning] |
== См. также == | == См. также == | ||
| Строка 71: | Строка 78: | ||
[[Категория:Нейронные сети]] | [[Категория:Нейронные сети]] | ||
| - | {{ | + | {{ЗаданиеВыполнено|Михаил Кузнецов|В.В.Стрижов|28 мая 2010|Mikethehuman|Strijov}} |
| - | [[Категория: | + | [[Категория:Практика и вычислительные эксперименты]] |
Текущая версия
Прореживание двухслойной нейронной сети (optimal brain damage) — метод упрощения структуры нейронной сети. Идея прореживания состоит в том, что из сети удаляются параметры, оказывающие малое влияние на ошибку аппроксимации. Таким образом, модель упрощается, а ошибка аппроксимации возрастает незначительно.
Содержание |
Постановка задачи
Задана обучающая выборка . Требуется решить задачу классификации с использованием двухслойной нейронной сети, настроив параметры сети - весовые матрицы
и
, соответствующие соответственно первому и второму слою. Посчитать гессиан
, где
- вектор параметров,
- функция стоимости; посчитать функцию выпуклости и упростить сеть, выбросив из нее параметры, соответствующие наименьшей степени выпуклости. Среднеквадратичная ошибка классификации
при этом не должна сильно возрасти.
Настройка нейронной сети
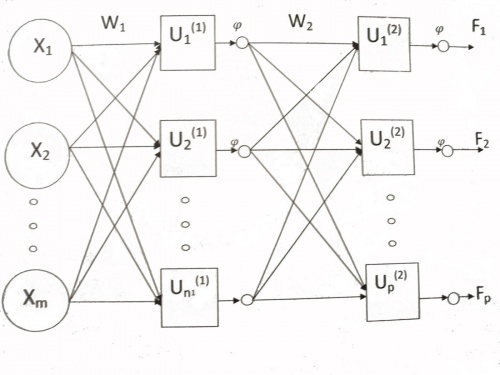
Двухслойная нейронная сеть состоит из одного скрытого слоя и выходного слоя. Входной слой - это объект со своим признаковым описанием . Первый и второй слои сети состоят из так называемых нейронов, или персептронов. Каждый нейрон вычисляет
-арную функцию вида
. В нашем случае
- сигмоидальная функция активации
. Значения признаков
поступают на вход первому (скрытому) слою сети с весовой матрицей
, выходы первого слоя поступают на вход второму с весовой матрицей
.На выходе второго слоя вычисляется вектор-функция
, где
- количество нейронов на втором слое. Необходимо настроить параметры сети, используя алгоритм обратного распространения (back propagation).
Введем функции ошибок: - нормированная среднеквадратичная ошибка,
- ошибка на конкретном объекте. Пусть
- вес, соединяющий нейрон
с нейроном
следующего слоя. Тогда коррекция веса, применяемая к
, определяется согласно правилу
, где
- локальный градиент нейрона
. Здесь
- выход
-го нейрона,
- значение, которое получает на вход функция активации, соответствующая
-му нейрону (
- количество его входов),
- темп обучения. Для выходного слоя
, и для него справедливо
.
Соответственно, для первого, скрытого, слоя справедлива формула обратного распространения
.
Отметим, что эти формулы взяты из книги С. Хайкина "Нейронные сети. Полный курс".
Алгоритм оптимального прореживания
Описание метода второго порядка приводится в статье Оптимальное прореживание нейронных сетей.
Локальная аппроксимация функции ошибки в окрестности стационарного положения:
где
— возмущение вектора параметров
,
— градиент
,
и
— матрица вторых производных
.
Необходимо минимизировать квадратичную форму по отношению к
при ограничении
. Для решения этой условной задачи строится лагранжиан
. Получаем, что оптимальное приращение вектора весов
, а соответствующее ему оптимальное значение лагранжиана для элемента
:
Основное отличие данного метода состоит в допущении, что матрица Гессе является диагональной. Таким образом, алгоритм немного видоизменяется:
Задана выборка , модель
, функция ошибки
. Для упрощения структуры сети выполняем следующие шаги:
1. настраиваем модель, получаем параметры .
2. пока значение ошибки не превосходит заранее заданного (3-5):
3. вычисляем гессиан согласно формуле
обозначим за аргумент функции активации нейрона
на слое
. Тогда частные производные на втором слое:
при
=
и равны 0 при
,
а на первом слое
и
4. вычисляем функцию выпуклости , находим
, соответствующее наименьшей степени выпуклости.
5. вес удаляется из сети
Примеры на модельных данных
Пример 1: выборка линейно разделима
На графике показаны результаты классификации. На первом и втором слое сети - по 5 нейронов, количество признаков - 4. Итого получается 45 весов. Видно, что алгоритм сработал без ошибок.
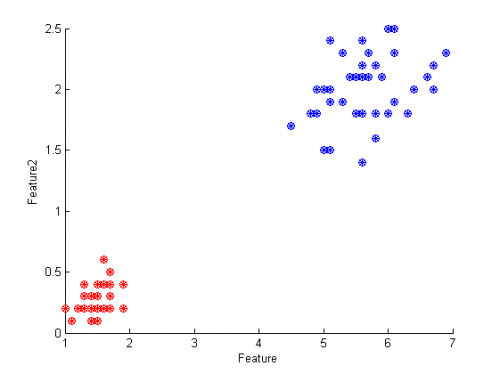
Ниже приведены графики функции выпуклости (одная кривая - зависимость функции выпуклости от суммы модулей параметров) и график зависимости ошибки от количества удаленных параметров.
Видно, что из сети с 45 параметрами можно удалить 18, практически не проиграв в качестве.
Пример 2: выборка линейно неразделима
Те же самые 45 весов. Алгоритм допустил 4 ошибки при классификации:
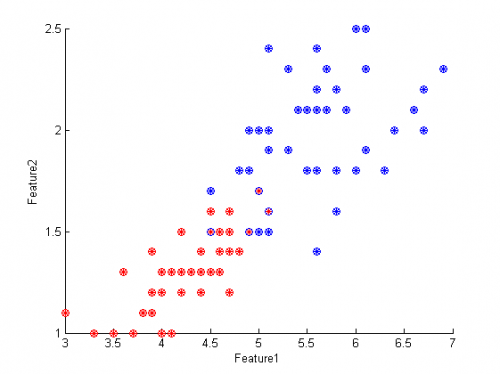
Графики функции выпуклости и количества ошибок:
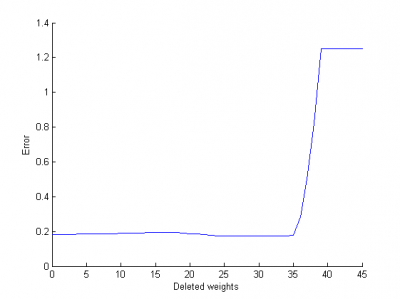
Результат прореживания здесь более наглядный: можно удалить 35 из 45 параметров без потери качества.
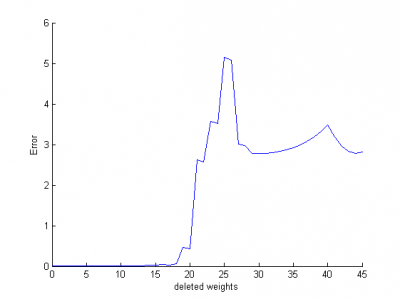
Для этого случая построим график функции ошибки ()в зависимости от параметров. На этом графике красным показаны параметры первого слоя, а синим - второго. В результате применения алгоритма OBD сначала удалялись те параметры, которые на графике видны плохо - именно они не оказывают большого значения на аппроксимацию.
Приведем график зависимости ошибки от количества удаленных параметров для тех же данных и 50 нейронов на каждом из слоев.
Исходный код
Скачать листинги алгоритмов можно здесь: [1]
См. также
- Оптимальное прореживание нейронных сетей
- Регрессионный анализ
- Вычисление матриц Якоби и Гессе
- Оптимальное прореживание нейронных сетей (пример)
Литература
- Хайкин С. Нейронные сети, полный курс. 2е издание, испр.
- К. В. Воронцов, Лекции по линейным алгоритмам классификации
| | Данная статья была создана в рамках учебного задания.
См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |