Анализ мультиколлинеарности (пример)

Материал из MachineLearning.

(Различия между версиями)

Версия 00:59, 29 сентября 2010

Мультиколлинеарность — тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров.

Содержание

1 Постановка задачи
2 Описание алгоритма
- 2.1 Фактор инфляции дисперсии (VIF)
- 2.2 Методика Belsley, Kuh, и Welsch (BKW)
  - 2.2.1 Алгоритм BKW
3 Вычислительный эксперимент
4 Исходный код
5 Смотри также
6 Литература

Постановка задачи

Задана выборка $D = \{ y_i,\mathbf{x}_i\}_{i=1}^n$ признаков и зависимой переменной. Рассматривается линейная регрессионная модель вида:

$y_i=\sum_{j=1}^m w_j x_{ij} + \varepsilon_i, i=1,\dots,n$ Предполагается, что вектор регрессионных невязок имеет нулевое математическое ожидание и дисперсию $\sigma^2$ . Требуется создать инструмент исследования мультиколлинеарности признаков (методики VIF, Belsley) и исследовать устойчивость модели на зависимость параметров от дисперсии случайной переменной.

Описание алгоритма

Фактор инфляции дисперсии (VIF)

В задаче восстановления регрессии фактор инфляции дисперсии (VIF) — мера мультиколлинеарности. Он позволяет оценить увеличение дисперсии заданного коэффициента регрессии, происходящее из-за высокой корреляции данных. Дисперсия $w_i$ может быть выражена как:

$D\hat{w}_j=\frac{\sigma^2}{(n-1)D x_j}\frac{1}{1-R_j^2}.$

Первая дробь связана с дисперсией невязок и дисперсией векторов признаков. Вторая — фактор инфляции дисперсии, связанный с корреляцей данного признака с другими:

$VIF_j=\frac{1}{1-R_j^2},$

где $R_j^2$ — коэффициент детерминации j-го признака относительно остальных - фактически он содержит информацию о том, насколько точно можно построить регрессию для j-го признака относительно остальных, т.е его зависимость от них. $R_j^2 \equiv 1-{\sum_{i=1}^n (x_{ij} - \hat{x}_{ij})^2 \over \sum_{i=1}^n (x_{ij}-\bar{\mathbf{x}}_j)^2},\.$

Равенство единице фактора инфляции дисперсии говорит об ортогональности вектора значений признака остальным. Если значение $VIF_j$ велико, то $1-R^2_j$ — мало, то есть $R_j^2$ близко к 1. Большие значения фактора инфляции дисперсии соответствуют почти линейной зависимости j-го столбца от остальных.

Методика Belsley, Kuh, и Welsch (BKW)

Диагностика коллинеарности BKW основана на двух элементах, относящихся к $n \times p$ матрице данных $X$ использующейся в линейной регрессии $y = X \beta + \epsilon$ : индексы обусловленности(the scaled condition indexes) и дисперсионные доли(the variance-decomposition proportions). Оба этих диагностических элемента могут быть получены из сингулярного разложения (SVD) матрицы $X$ : $X=UD{V^{T}}$ , где ${U}^{T}U={V}^{T}V={I}_{p}$ и $D$ - диагональная с неотрицательными элементами ${\mu}_{1},...,{\mu}_{p}$ называющимися сингулярными числами $X$ . Индексы обусловленности это:
${\eta}_{k}\equiv\frac{{\mu}_{max}}{{\mu}_{k}}$ , $k=1,...,p$
${\eta}_{k} \geq 0$ для всех $k$ . Большое значение ${\eta}_{k}$ указывает на зависимость близкую к линейной между признаками и чем больше ${\eta}_{k}$ тем сильнее зависимость. Дисперсионные доли находятся из того факта, что используя SVD ковариационная матрица метода наименьших квадратов $b=(X^{T}X)^{-1}X^{T}y$ может записана как:

(3)

$V(b)={\sigma}^{2}(X^{T}X)^{-1} = {\sigma}^{2}V D^{-2} V^{T}$
где ${\sigma}^{2}$ это дисперсия возмущения $\varepsilon$ . Таким образом дисперсия $k$ -го регрессионного коэффициента ${b}_{k}$ это $k$ -й диогональный элемент (3):

(4)

$\mbox{var}({b}_{k})={\sigma}^{2} \sum_{j} {\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}}$
где ${\mu}_{j}$ - сингулярные значения $X$ и $V\equiv({\upsilon}_{ij})$ . Определим $k, j$ -е дисперсионное соотношение как долю дисперсии $k$ -го регрессионного коэффициента связанная с $j$ -м компонентом его разложения (4). Доля считается как:
${\phi}_{kj}\equiv\frac{{\upsilon}^{2}_{kj}}{{\mu}^{2}_{j}}$ , ${\phi}_{k}\equiv\sum^{p}_{j=1} {\phi}_{kj}$ , $k=1,...,p$
Дисперсионное соотношение:
${\pi}_{jk}\equiv\frac{{\phi}_{kj}}{{\phi}_{k}}$ , $k,j=1,...,p$
Данные удобно представить в виде таблицы:

Condition index	$var({b}_{1})$	$var({b}_{2})$	$...$	$var({b}_{p})$
${\eta}_{1}$	${\pi}_{11}$	${\pi}_{12}$	...	${\pi}_{1p}$
${\eta}_{2}$	${\pi}_{11}$	...	...	${\pi}_{2p}$
.	.	.		.
.	.	.		.
.	.	.		.
${\eta}_{p}$	${\pi}_{p1}$	${\pi}_{11}$	...	${\pi}_{pp}$

Перед использованием BKW необходимо отмасштабировать матрицу $X$ . Стандартно применяется приведение столбцов к одинаковой длинне(норму). Будем рассматривать отмасштабированные индексы обусловленности $\stackrel{\sim}{{\eta}_{i}}(X)$ :
$X=[{X}_{1}\cdot\cdot\cdot{X}_{p}]<tex><br/> <tex>{s}_{i}\equiv{({X}^{T}_{i}{X}_{i})}^{-1/2}$
$S\equiv \mbox{diag}({s}_{1},...,{s}_{p})$
$\stackrel{\sim}{\eta}\equiv {\eta}_{i}(XS)$ , $i=1,...,p$

Алгоритм BKW

1. Стандартизация столбцов матрицы.
2. Вычисление индексов обусловленности и дисперсионных долей.
3. Определение количества зависимостей.
Превышение индексом обусловленности выбраного заранее порога означает наличие зависимости между признаками. Относительная сила зависимости определяется положение значения индекса обусловленности в прогресии 1, 3, 10, 30, 100, 300, 1000 итд.
4. Определение признаков участвующих в зависимости. 2 случая :
1) Только один достаточно большой индекс обусловленности - тогда возможно определение участвующих в зависимости признаков из дисперсионных долей: признак считается вовлеченным если его дисперсионная доля связанная с этим индексом превышает выбранный порог ${\pi}^{*}$ (обычно 0.25).
2) Есть несколько больших индексов обусловленности. В этом случае вовлеченность признака в зависимость определяется по сумме его дисперсионных долей отвечающих большим значениям индекса обусловленности - когда сумма превышает порог ${\pi}^{*}$ признак участвует как минимум в одной линейной зависимости.

Вычислительный эксперимент

В эксперименте используются модельные данные, для которых вычисляется VIF и матрица Belsley в зависимоти от параметра определяющего степень коллинеарности между признаками. Зависимость VIF и индексов обусловленности показана на графиках. Остальная часть таблицы BKW раскрашивалась (от темно-синего для 0 к темно-красному для 1) и создавалось видео показывающее ее изменение при параметре от 0 до 1.

Пример 1

Используются 2 ортогональных признака $x_1$ , $x_2$ и третий $y_1$ зависящий от параметра $k$ . При параметре равном 0 все признаки ортогональны, при его увеличении $y_1$ приближается к $x_1$ , вплоть до полной коллинеарности при $k=1$ . Зависимость VIF от параметра:

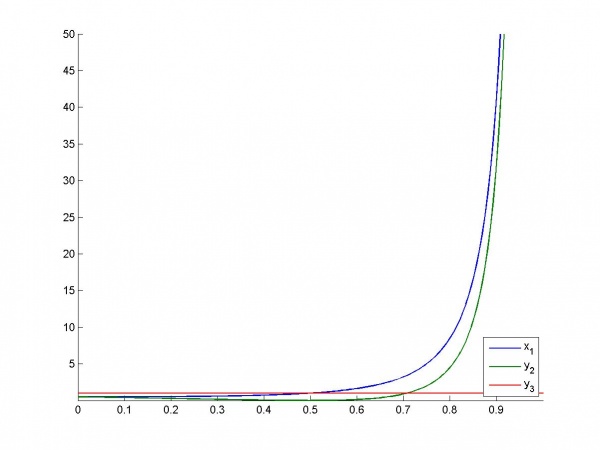
Как видно из графика VIF $x_1$ и $y_1$ растет вплоть до бесконечности при $k=1$ , VIF $x_2$ при этом не изменен и равен 1.
Зависимость индексов обусловленности от $k$ :

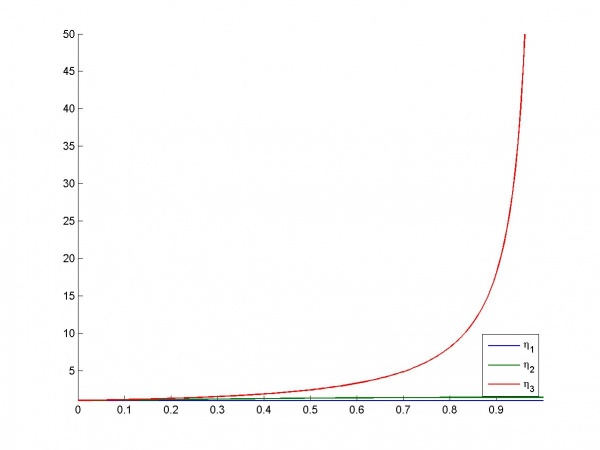
Таблица дисперсионных долей:

Видно что $x_1$ и $y_1$ связаны усиляющейся зависимостью, и что других связей нет.

Пример 2

Используется неизменный признак $x_1$ и зависящие от параметра $y_1$ , $y_2$ , $y_3$ . При параметре равном 0 все признаки ортогональны, при его увеличении $y_1$ , $y_2$ , $y_3$ одновременно начинают приближаться к $x_1$ вплоть до полной коллинеарности при $k=1$ . Зависимость VIF от параметра:

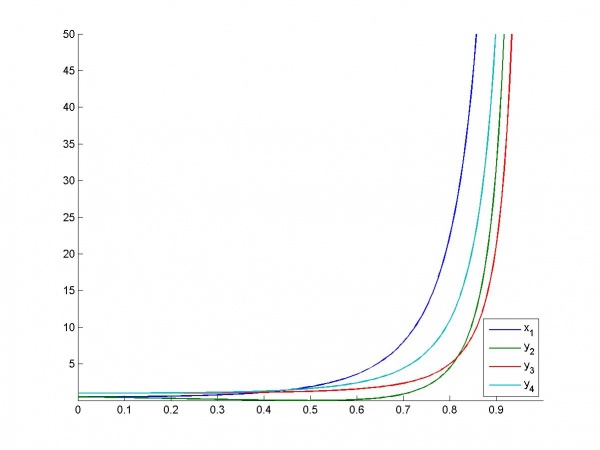
Зависимость индексов обусловленности от $k$ :

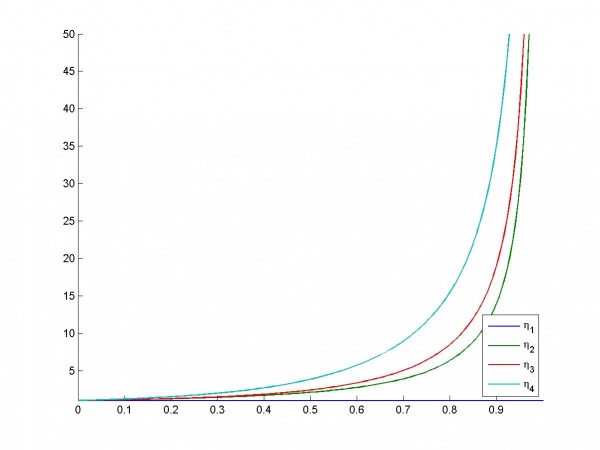
Таблица дисперсионных долей:

Наблюдаются 3 зависимости - в самой сильной участвуют все 4 признака, во второй $y_1$ и $y_3$ , и в самой слабой $y_1$ и $y_1$ .

Пример 3

Используется неизменные признаки $x_1$ , $x_2$ и зависящие от параметра $y_1$ , $y_2$ , $y_3$ . ПРи параметре равном 0 все признаки ортогональны, при его увеличении $y_1$ , $y_2$ приближаются к $x_1$ , $y_3$ - к $x_2$ вплоть до полной коллинеарности при $k=1$ .
Зависимость VIF от параметра:

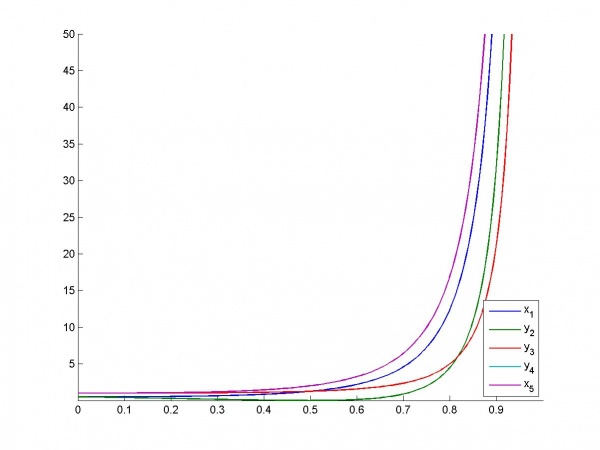
Зависимость индексов обусловленности от $k$ :

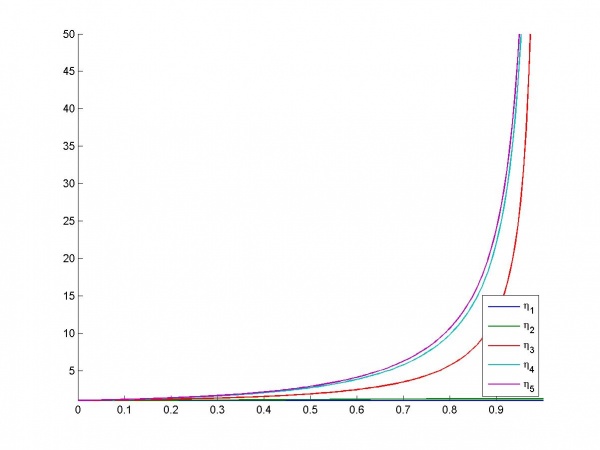
Таблица дисперсионных долей:

Наблюдается 2 основных зависимости - между $x_1$ , $y_1$ , $y_2$ и вторая между $x_2$ , $x_3$ .

Исходный код

Cкачать листинги алгоритмов можно здесь [1]

Смотри также

Литература

Gianfranco Galmacci, Collinearity Detection in Linear Regression. Computational Economics 9:215-227, 1996.
D. A. Belsley, A Guide to Using the Collinearity Diagnostics. Computer Science in Economics and Management 4: 33-50, 1991.

Данная статья является непроверенным учебным заданием.

Студент: Участник:Сунгуров Дмитрий

Преподаватель: Участник:В.В.Стрижов

Срок: 28 мая 2010

До указанного срока статья не должна редактироваться другими участниками проекта MachineLearning.ru. По его окончании любой участник вправе исправить данную статью по своему усмотрению и удалить данное предупреждение, выводимое с помощью шаблона {{Задание}}.

См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе.

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D0%BC%D1%83%D0%BB%D1%8C%D1%82%D0%B8%D0%BA%D0%BE%D0%BB%D0%BB%D0%B8%D0%BD%D0%B5%D0%B0%D1%80%D0%BD%D0%BE%D1%81%D1%82%D0%B8_%28%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D1%80%29»

Категории: Непроверенные учебные задания | Практика и вычислительные эксперименты | Линейная регрессия

@@ Строка 80: / Строка 80: @@
 Зависимость VIF от параметра:<br/>
 [[Изображение:plot3vif.jpg|600px]]<br/>
-Как видно из графика VIF <tex>x_1</tex> и <tex>y_1</tex> растет вплоть до бесконечности при <tex>k=1</tex>, VIF <tex>x_2</tex> при это не изменен и равен 1.<br/>
+Как видно из графика VIF <tex>x_1</tex> и <tex>y_1</tex> растет вплоть до бесконечности при <tex>k=1</tex>, VIF <tex>x_2</tex> при этом не изменен и равен 1.<br/>
 Зависимость индексов обусловленности от <tex>k</tex>:<br/>
 [[Изображение:plot3sci.jpg|600px]]<br/>
@@ Строка 88: / Строка 88: @@
  |}<br/>
 Видно что <tex>x_1</tex> и <tex>y_1</tex> связаны усиляющейся зависимостью, и что других связей нет.
 ===Пример 2===
 Используется неизменный признак <tex>x_1</tex> и зависящие от параметра <tex>y_1</tex>, <tex>y_2</tex>, <tex>y_3</tex>. При параметре равном 0 все признаки ортогональны, при его увеличении <tex>y_1</tex>, <tex>y_2</tex>, <tex>y_3</tex> одновременно начинают приближаться к <tex>x_1</tex> вплоть до полной коллинеарности при <tex>k=1</tex>.