Эмпирическое распределение

Материал из MachineLearning.

(Различия между версиями)
Перейти к: навигация, поиск
Строка 1: Строка 1:
-
'''Эмпирическая функция распределения''' — естественное приближение теоретической [[Функция распределения|функции распределения]] данной [[Случайная величина|случайной величины]], построенное по выборке.
+
'''Эмпирическая функция распределения''' (выборочная функция распределения) — естественное приближение теоретической [[Функция распределения|функции распределения]] данной [[Случайная величина|случайной величины]], построенное по выборке.
== Определения ==
== Определения ==
Строка 22: Строка 22:
[[Функция распределения|функция распределения]] случайной величины <tex>x</tex>), а последовательность <tex>\left(I_{\left\{x_1\leq x\right\}},\ldots,I_{\left\{x_m\leq x\right\}}\right)</tex> - схема Бернулли с вероятностью успеха <tex>F(x)</tex>, то по отношению к этой последовательности <tex>\hat{F}_m(x)</tex> есть частота попаданий левее x.
[[Функция распределения|функция распределения]] случайной величины <tex>x</tex>), а последовательность <tex>\left(I_{\left\{x_1\leq x\right\}},\ldots,I_{\left\{x_m\leq x\right\}}\right)</tex> - схема Бернулли с вероятностью успеха <tex>F(x)</tex>, то по отношению к этой последовательности <tex>\hat{F}_m(x)</tex> есть частота попаданий левее x.
 +
Из сказанного вытекает, что эмпирическое распределение служит естественным приближением к теоретической функции распределения.
===Математическое ожидание и дисперсия эмпирического распределения===
===Математическое ожидание и дисперсия эмпирического распределения===
Математическое ожидание эмпирической функции распределения
Математическое ожидание эмпирической функции распределения
Строка 33: Строка 34:
===Асимптотические свойства эмпирической функции распределения===
===Асимптотические свойства эмпирической функции распределения===
-
# По [[Закон больших чисел|усиленному закону больших чисел]] <tex>\hat{F}_m(x)</tex> сходится ''почти наверное'' к теоретической функции распределения <tex>F(x).</tex>
+
1. По [[Закон больших чисел|усиленному закону больших чисел]] <tex>\hat{F}_m(x)</tex> сходится ''почти наверное'' к теоретической функции распределения <tex>F(x)</tex>:
-
== Замечания ==
+
::<tex>\hat{F}_m(x)\to^ F(x)</tex> ''почти наверное'' при <tex>m \rightarrow \infty.</tex>
 +
2. Выборочная функция распределения является ''асимптотически нормальной'' оценкой функции распределения <tex>F(x)</tex> при условии, что <tex>0< F(x)< 1,~ \forall x \in \mathbb{R}</tex>:
 +
::<tex>\sqrt{n}\left(\hat{F}_m(x)-F(x)\right) \to^{P} N\left(0,F(x)(1-F(X))\right)</tex> при <tex>m \to \infty.</tex>
 +
 
 +
 
 +
== Литература ==
 +
 
 +
# {{книга
 +
|автор = Лагутин М.Б.
 +
|заглавие = Наглядная математическая статистика.
 +
|издательство = М.: Бином. Лаборатория знаний.
 +
|год = 2009
 +
|страниц = 472
 +
}}
 +
# {{книга
 +
|автор = Крамер Г.
 +
|заглавие = Математические методы статистики.
 +
|издательство = М.: Мир.
 +
|год = 1975
 +
|страниц = 648
 +
}}
 +
 
 +
==Ссылки==
 +
*[http://ru.wikipedia.org/wiki/%D0%92%D1%8B%D0%B1%D0%BE%D1%80%D0%BE%D1%87%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F Выборочеая функция распределения] (Википедия)
 +
 
 +
[[Категория:Прикладная статистика]]
 +
[[Категория:Математическая статистика]]
 +
[[Категория:Энциклопедия анализа данных]]

Версия 13:04, 6 января 2010

Эмпирическая функция распределения (выборочная функция распределения) — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.

Содержание

Определения

Пусть задана случайная выборка x^m=\left(x_1,\ldots,x_m\right) наблюдений x_i \in X. Построим по выборке ступенчатую функцию \hat{F}_m(x), возрастающую скачками величины \frac{1}{m} в точках x_{(i)}. Построенная функция называется эмпирической функцией распределения. Для задания значений в точках разрыва формально определим её так:

\hat{F}_m(x)\;=\;\frac{1}{m}\sum_{i=1}^m I_{\left\{x_i\leq x\right\}}.

Замечание: при этом эмпирическая функция непрерывна справа.

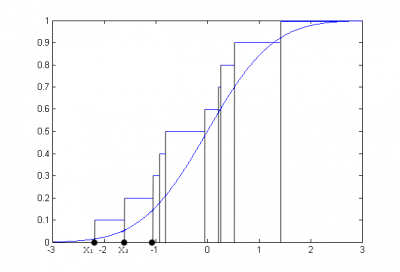
На рисунке представлена функция стандартного нормального распределения и эмпирическая функция распределения, построенная по выборке из 10 случайных наблюдений из стандартного нормального закона.

Пример эмпирической функции распределения, построенной по выборке из 10 наблюдений.
Пример эмпирической функции распределения, построенной по выборке из 10 наблюдений.

Свойства эмпирической функции распределения

Эмпирическое распределение для фиксированного 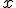x

Поскольку случайная величина I_{\left\{x_i\leq x\right\}} имеет распределение Бернулли с вероятностью успеха F(x) (где F(x) - теоретическая функция распределения случайной величины x), а последовательность \left(I_{\left\{x_1\leq x\right\}},\ldots,I_{\left\{x_m\leq x\right\}}\right) - схема Бернулли с вероятностью успеха F(x), то по отношению к этой последовательности \hat{F}_m(x) есть частота попаданий левее x.

Из сказанного вытекает, что эмпирическое распределение служит естественным приближением к теоретической функции распределения.

Математическое ожидание и дисперсия эмпирического распределения

Математическое ожидание эмпирической функции распределения

  • E\left[\hat{F}_m(x)\right] = F(x),

таким образом эмпирическое распределение является несмещённой оценкой теоретической функции распределения F(x).

Дисперсия эмпирического распределения

  • D\left[\hat{F}_m(x)\right]=\frac{F(x)\left(1-F(x)\right)}{m}.

Асимптотические свойства эмпирической функции распределения

1. По усиленному закону больших чисел \hat{F}_m(x) сходится почти наверное к теоретической функции распределения F(x):

\hat{F}_m(x)\to^ F(x) почти наверное при m \rightarrow \infty.

2. Выборочная функция распределения является асимптотически нормальной оценкой функции распределения F(x) при условии, что 0< F(x)< 1,~ \forall x \in \mathbb{R}:

\sqrt{n}\left(\hat{F}_m(x)-F(x)\right) \to^{P} N\left(0,F(x)(1-F(X))\right) при m \to \infty.


Литература

  1. Лагутин М.Б. Наглядная математическая статистика.. — М.: Бином. Лаборатория знаний., 2009. — 472 с.
  2. Крамер Г. Математические методы статистики.. — М.: Мир., 1975. — 648 с.

Ссылки

Источник — «http://www.recognition.su/wiki/index.php?title=%D0%AD%D0%BC%D0%BF%D0%B8%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5»
Личные инструменты